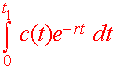Integration by Parts

 Derivation of Integration by Parts

Recall the product rule:

        (uv)' = u' v + uv' 

or

        uv' = (uv)' - u' v

Integrating both sides, we have that

       uv' dx     =     (uv)' dx  -   u' v dx

        =    uv   -   u' v dx.

 

 

Theorem:  Integration by Parts

Let u and v be differentiable functions, then

         

 

 

Examples

Integrate

          

Solution

We use integration by parts.  Notice that we need to use substitution to find the integral of ex.

 
u = x dv= e3x dx
du = dx v = 1/3 e3x

Hence we have

       

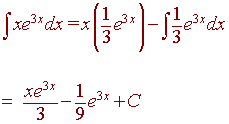
Exercise

Evaluate

       x ln x dx        (x^2 / 2) ln x - 1/4 x^2 + C

 

 

Integration By Parts Twice

Example 

Evaluate

         x2 ex dx

We use integration by parts

 
u = x2   dv = ex dx
du = 2x dx v = ex

We have

        x2ex - 2xex dx     =     x2ex - 2xex dx

Have we gone nowhere?  Now we now use integration by parts a second time to find this integral

 
u = x   dv = ex dx
du = dx v = ex

We get

         x2ex   -   2xex  +  2ex dx

        =     x2ex   -   2xex  +   2ex + C

 

Other By Parts

Occasionally there is not an obvious pair of u and dv.  This is where we get creative.

 

Example:  

Find

        ln x dx

What should we let u and dv be?  Try

 
u = ln x dv = dx
du =  1/x dx v =  x

We get

        x lnx   -   dx      =    x lnx  -  x  +  C

 

When to Use Integration By Parts

  1. When u-substitution does not work


  2. When there is a mix of two types of functions such as an exponential and polynomial, polynomial and log, etc.


  3. With  ln x.


  4. When all else fails.

 

Evaluating a Definite Integral

We can use integration by parts to evaluate definite integrals.  We just have to remember that all terms receive the limits.

 

Example

Evaluate

       

 

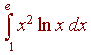
Solution

Use integration by parts

 
u = ln x dv = x2 dx
du =  1/x dx v =  1/3 x3

We get

       

 

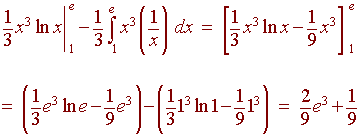
Application:  Present Value

Your patent brings you a annual income of 3,000 t dollars where t is the number of years since the the patent begins.  The patent will expire in 20 years.  A business has offered to purchase the patent from you.  How much should you ask for it?  Assume an inflation rate of 5%.

This question is a present value problem.  Since there is inflation, your later earnings will be worth less than this year's earnings.  The formula to determine this is given by

 

        

Present Value Formula

If c(t) is the continuous annual income over t1 years with an inflation rate r, then the present value can by found by 

                   

 

For our example, we have

        c(t)  =  2000 t        r  =  0.05        t1  =  20

We integrate

       

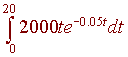
Use integration by parts and note that with the substitution

        u  =  -0.05t        du  =  -0.05dt

or

        -20du  =  dt

we get

       

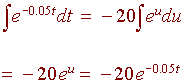
so that

 
u = 2000t dv = e-0.05t dt
du =  2000 dt v =  -20e-0.05t

This gives us

       

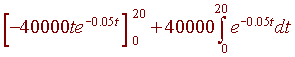
We have already found the antiderivative for this last integral.  We have

       

You should ask for $211,393.

 

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions