LOGARITHMS

The inverse of the exponential function--  The Natural Logarithm

The graph of 

        y  =  e^x 

clearly shows that it is a one to one function, hence an inverse exists.  We call this inverse the natural logarithm.  and write it as

        y  =  ln x

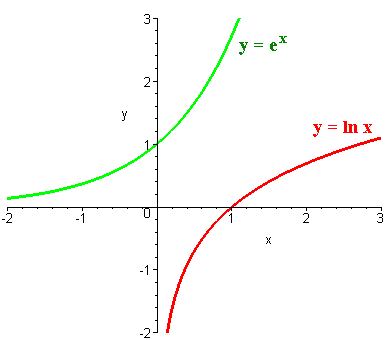
Below is the graph of 

        y = e^x  

and 

        y   =  ln x 

By definition, they are reflections of each other across the line y  =  x. 

Inverse Properties of Logs

Since logs and exponents cancel each other we have:

        e^{ln x}  =  x 

and

            ln e^x  =  x

Example

        e^{ln 3}  =  3            and            ln(e⁵)  =  5

Three Properties of Logs

        Property 1:  ln (uv)  = ln u  +  ln v    (The Product to Sum Rule)

        Property 2:  ln (u/v) = ln u  -  ln v    (The Quotient to Difference Rule)

        Property 3:  ln u^r   =  r ln u                    (The Power Rule)

Example:

Expand:  

        ln (xy²/z)

by property 2 we have:

        ln (xy²) -  ln z

by property 1 we have

        ln x + ln y²  - ln z

By property 3 we have

        ln x + 2 ln y - ln z

Exercise

Try to expand

Example

Write as a single logarithm:

        4ln x - 1/2ln y  + ln z

Solution

We first use property 3 to write:

        ln x⁴ - ln y^1/2  + ln z

Now we use property 2:

                x⁴  
        ln               +  ln z
              y^1/2  

Finally, we use property 3:

                x⁴ z 
        ln               +  ln z
              y^1/2  

Exercise

Write the following as a single logarithm:

        1/3 ln x  +  2 ln y   -  3 ln z

Example

Suppose that  

        ln 3 = 1.10 

and that 

        ln 5 = 1.61

Find 

        ln 45

Solution

Since 

        45 = (5)(3²)

We have

        ln 45  =  ln (5)(3²)  =  ln 5 + ln 3²

        =   1.61 + 2 ln 3

        =  1.61 + 2 (1.10)  =  3.81

Exponential Equations

The key to solving equations is to know how to apply the inverse of a function.  When we have an exponential equation, we will use the natural logarithm to cancel the exponential.

Example

Find k if

        34  =  e^10k

Solution

Take the natural logarithm of both sides

        ln 34  =  ln e^10k

Now use the inverse property 

        ln 34  =  10k

Finally divide by 10

           ln 34  
                        =  k  =  0.3526
             10

Carbon Dating

All living beings have a certain amount of radioactive carbon C₁₄ in their bodies.  When the being dies the C₁₄ slowly decays with a half life of about 5600 years.  Suppose a skeleton is found in Tahoe that has 42% of the original C₁₄.   When did the person die?

Solution

We can use the exponential decay equation:

        y  =  Ce^kt 

After 5600 years there is 

        C/2 

C₁₄ left.  Substituting, we get:

        C/2  =  Ce^k(5600)

Dividing by C,

        1/2  =  e^5600k

Take ln of both sides,

        ln(0.5)  =  5600k

so that

                   ln(0.5)
        k  =                 =  -0.000124
                   5600

The equation becomes

        y  =  Ce^-0.000124t 

To find out when the person died, substitute 

        y  =  0.42C 

and solve for t:

        0.42C  =  Ce^-0.000124t

Divide by C,

        0.42  =  e^-0.000124t

Take ln of both sides,

        ln(0.42)  =  -0.000124t

Divide by -0.000124

                 ln(0.42)
        t =                     = 6995
               -0.000124

The person died about 7,000 years ago.

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions