e
Definition of e
There is a special base of an exponential that plays a particularly important role in mathematics. One way of defining e is with the compound interest formula
|
A = P(1 + r/n)nt |
where A corresponds to the amount in the account after t years in a bank that gives an annual interest rate r compounded n times per year. For example if n = 4 we say that the account is compounded quarterly and if n = 365 then the account is compounded daily. The more often the account is compounded, the faster the interest grows.
If we let
r = 1 P = 1 t = 1 and x = 1/n
then the compound interest formula gives
f(x) = (1 + x)1/x
We can interpret x as the fraction of a year that the interest compounds. If this fraction goes to 0 then we can construct the following table:
| x | 0.1 | 0.01 | 0.001 | 0.0001 | 0.00001 |
| f(x) | 2.59374 | 2.70481 | 2.71692 | 2.71814 | 2.71827 |
This function seems to converge to a number, which we call e.
|
|
Continuous Interest
For continuously compounded interest, we have the formula:
|
A = Pert |
Inflation Example
With an 8% rate of inflation in the health industry, how much will health
insurance cost in 45 years if currently I pay $200 per month?
Solution
We have
r =
.08 P =
200 and
t = 45
So that
A = 200e(.08)(45) = $7319 per month!
Population Growth Models
One of the simplest models for population growth arises from the assumption that the rate of growth is proportional to the current population. Later we will show that under this assumption, the population P at time t is given by
P = C0 ekt
Where C0 is the initial population and k is a proportionality constant.
Example
In 1960 two-hundred plants from Europe were brought into the US for landscaping. Assuming exponential growth with a growth constant of 0.1, how many plants will be in the US by the year 2050?
Solution
We let t = 0 correspond to the year 1960. Then C0 = 200. The exponential growth model gives
P = 200 e0.1t
Next, 2050 corresponds to t = 90. So that
P(90) = 200 e(0.1)(90) = 1,620,616
There will be 1,620,616 of these foreign plants by the year 2050. The graph is shown below.
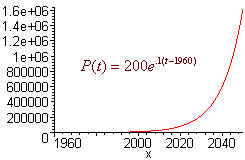
The exponential model has a serious flaw. It assumes that the population will continue growing regardless of space and nutrients. A more realistic model will account for the fact that there is a carrying capacity, that is a population that cannot be surpassed. This model is called the logistics equation and is given by
![]()
where a, b, and k are positive constants.
Example
The human population (in billions of people) on earth can be modeled by the logistics growth curve
50
P =
1 + 11.5e-0.0225t
where t is the year since 1970. What will the population be in 2010? What is the human carrying capacity of the earth?
Solution
To determine the population in 2010, we see that 2010 corresponds to t = 40. We plug this t in and use a calculator to get
50
P(40) =
= 8.8
1 + 11.5e-0.0225(40)
There will be approximately 8.8 billion people on earth in the year 2010.
To find the carrying capacity, we find the limit of the population as time approaches infinity. From the equation we see that the exponential term goes to 0 since the exponent is negative. Hence the carrying capacity L is
50
L =
= 50
1 + 0
Thus the carrying capacity is 50 billion people.
Back to the Math 116 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions