MATH
115 PRACTICE MIDTERM II
Please work out each of the given problems.
Credit will be based on the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Find
![]() for the following
for the following
A)
1 - x2
y =
1 + x2
![]()
We use the quotient rule we have
(1 + x2)(-2x) - (1 - x2)(2x)
y' =
(1 + x2
)2
![]()
Just for fun we can simplify this as
-2x
- 2x3 - 2x + 2x3
- 4x
=
(1 + x2
)2
B) y = (2 - 3x)14
We use the chain rule. The inside function is
u = 2 - 3x
which has derivative
u ' = -3x
and the outside function is
y = u14
which has derivative
y ' = 14u13
Multiplying gives
u' y ' = (-3x)(14u13) = -42x u13
Finally re-substitute to get
y ' = -42x(2 - 3x)13
C)
y = x2 sin(x - x4 )
We need to use both the chain rule and the product rule. First use the product rule
y ' = x2 [sin(x - x4)] ' + 2x sin(x - x4)
We now need to find the derivative of
z = sin(x - x4)
We use the chain rule with
u = x - x4 z = sin u
Taking derivatives gives
u' = 1 - 4x3 z ' = cos u
which gives
z' = (1 - 4x3)cos u = (1 - 4x3)cos(1 - 4x3)
Putting this all together gives
y ' = x2 (1 - 4x3)cos(1 - 4x3) + 2x sin(x - x4)
D)
3x2 - x2y + y4
= -3
We use implicit differentiation for this one. Notice that we need the product rule for the second term. Also notice that when we take a derivative of an expression of y with respect to x, we need to multiply by y '. Taking derivatives of both sides
6x - (2xy + x2y ' ) + 4y3y ' = 0
6x - 2xy - x2y ' + 4y3y ' = 0
Now solve for y ' by getting all the non-y ' terms on the right. We have
-x2y ' + 4y3y ' = 2xy - 6x
Next factor out a y '
(4y3 - x2 ) y ' = 2xy - 6x
Divide to get
2xy - 6x
y '
=
4y3 - x2
PROBLEM 2
![]()
First convert the square root to an exponent
y = x(1 - x)1/2
Next, use the product rule in conjunction with the chain rule to find the first derivative
y ' = x [(1 - x)1/2 ] ' + (1)(1 - x)1/2
To find the derivative of
z = (1 - x)1/2
we use the chain rule with
u = 1 - x z = u1/2
u' = -1 z' = 1/2 u -1/2
This gives
z' = (-1)(1/2 u -1/2 ) = -1/2 (1 - x)-1/2
Putting this all together gives
y' = 1/2 x (1 - x) -1/2 + (1 - x)1/2
Next, we find the second derivative. We use the product rule on the first term and the chain rule on the second (which we have already done in this problem).
y '' = 1/2 x [(1 - x) -1/2 ] ' + 1/2 (1 - x)1/2 - 1/2 (1 - x) -1/2
We need only find the derivative of
z = (1 - x) -1/2
we use the chain rule with
u = 1 - x z = u -1/2
u' = -1 z' = -1/2 u -3/2
This gives
z' = (-1)(-1/2 u -1/2 ) = 1/2 (1 - x)-3/2
Putting this all together gives
y '' = 1/4 x (1 - x) -3/2 + 1/2 (1 - x)1/2 - 1/2 (1 - x) -1/2
PROBLEM 3
A zoo keeper plans to build a rectangular cage for
her newly arrived panda bears. The
front of the cage is to be made of glass at a cost of $100
per foot and the other three sides of the cage are to be made of concrete
costing $50 per foot.
If the zoo keeper has $3000 to spend on the
cage, what dimensions should the cage be so as to maximize the area of the cage?
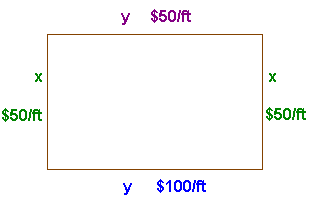 The
diagram is shown to the right. The area of the cage is
The
diagram is shown to the right. The area of the cage is
A = xy
and the cost is given by
3000 = 50y + 100y + 50x + 50x
100x + 150y = 3000
Solving for x gives
100x = 3000 - 150y
Now dividing by 100 gives
x = 30 - 1.5y
Substitute into the area equation to get
A = (30 - 1.5y)y = 30y - 1.5y2
Since we want the maximum area, we take a derivative to get
A' = 30 - 3y
Setting the derivative equal to zero gives
30 - 3y = 0 y = 10
The first derivative test shows that this is a maximum since
A'(9) = 3 > 0 and A'(11) = -3 < 0
Now find x to get
x = 30 - 1.5(10) = 15
We can say that the front and back of the cage should be 10 feet and the two sides should be 15 feet to maximize area.
PROBLEM 4
The nearby sewage plant has just announced that it had a chlorine gas spill. The gas cloud is in the shape of a hemisphere with equator on the ground. The volume of the cloud is expanding at a rate of 10,000 cubic feet per minute. How fast is the radius of the cloud moving by the time the cloud has reached the campus gym which is 200 feet away? (Hint: the volume of a hemisphere is
2p r3
V
=
3
and you want to find out how fast the radius is changing.
This is a related rates problem. We take the derivative with respect to t of both sides
dV/dt = 2p r2 dr/dt
We are given that
dV/dt = 10000 and r = 200
Plugging in gives
10000 = 2p (200)2 dr/dt
10000 = 80000p dr/dt
dividing gives
dr 1
=
dt
8p
We can conclude that the chlorine gas cloud is moving at a rate of 1/ 8p feet per second by the time it reaches the gym.
PROBLEM 5
Without the use of the graphing capability of a graphing calculator, use calculus to find where the following function is increasing and decreasing. Also use the first derivative test to locate and classify the relative extrema.
y = 2x3 - 3x2
We take the first derivative
y' = 6x2 - 6x = 6x(x - 1)
The first derivative is zero when x = 0 or x = 1. We test the derivative at points to the left of 0, between 0 and 1, and to the right of 0.
| x | -1 | 1/2 | 2 |
| y ' | 12 | -3/2 | 12 |
Since the derivative is positive to the left of 0 and to the right of 1, the function is decreasing there. Since the derivative is negative between 0 and 1, the function is increasing there.
Decreasing: (0,1)
Increasing:
(- ![]() , 0)
U ( 1 ,
, 0)
U ( 1 , ![]() )
)
On the number line it looks like
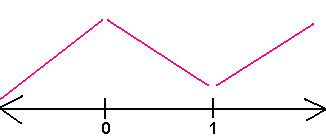
By the first derivative test, we can conclude that there is a relative maximum at x = 0 and a relative minimum at x = 1.
PROBLEM 6
The profit made is selling x automobiles can be modeled by the equation
P = x2(8x2 + x) -1/2
Find the marginal profit when x = 1.
We need to find the derivative. We use the product rule and the chain rule.
P' = x2 [(8x2 + x) -1/2] '
+ (2x)(8x2 + x) -1/2
Now use the chain rule to find the derivative
u = 8x2 + x y = u -1/2
u' = 16x + 1 y' = -1/2 u -3/2
y' = (16x + 1)(-1/2 u -3/2) = (16x + 1)(-1/2 (8x2 + x) -3/2 )
Substitute this in to get
P' = -1/2 x2 (16x
+ 1) (8x2 + x) -3/2 + (2x)(8x2 + x) -1/2
Finally, plug in 1 for x to get
P'(1) = -1/2 (17)
(9) -3/2 + (2)(9) -1/2
The calculator gives .3519.
PROBLEM 7
y = x3 - 12x
on the closed interval [0,3].
SolutionWe take the derivative to get
y' = 3x2 - 12 = 3(x2 - 4) = 3(x - 2)(x + 2)
The critical points are x = -2 and x = 2. Notice that -2 is not in the interval [0,3], hence we ignore this one. We plug in the critical point and the endpoints into the original equation to find the absolute extrema.
| x | 0 | 2 | 3 |
| y | 0 | -16 | -9 |
We see that the largest value from y is 0 and the smallest is -16. The function has an absolute minimum of -16 at x = 2 and an absolute maximum of 0 at 0.