Please work out each of the given problems.
Credit will be based on the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Please answer the following true or false.
If false, explain why or provide a counter example.
If true, explain why.
A) If
f(x) = x2 - x
then the tangent line to
f(x) at x = 2 is parallel to the line y
= 3x + 7.
Solution
The slope of the tangent line is the derivative. We have
f '(x) = 2x - 1
f '(2) = 2(2) - 1 = 3
The slope of the line y = 3x + 1 is also 3. Since lines are parallel if and only if they have the same slope, we can say True.
B) If
x2 - 4
f(x) =
x + 2
then f(x) is
continuous at x = -2
Solution
False, the denominator is zero at x = -2 which makes it continuous, even though the limit exists.
C) If a
function f has a limit L at x
= c, and f(c) = L, then the function is
differentiable at x = c.
False, this is the definition of continuity not differentiability. For example
f(x) = |x|
is not differentiable at x = 0 but is continuous there.
PROBLEM 2 Explain in
your own words what the difference between continuity and differentiability is.
Solution
Continuity means you can draw the curve without your pencil leaving the paper, while for a function to be differentiable, it shouldn't have any sharp edges either.
(Of course, your own words should be different then mine, but imply the same meaning.)
PROBLEM 3
The graph of y = f(x) is
given below.
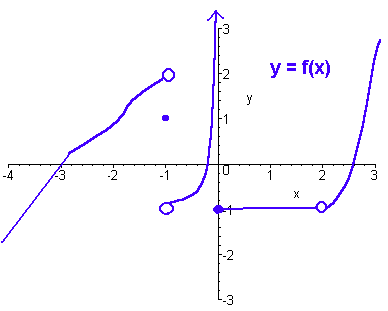
A) Evaluate
the following limits if they exist:
i)
![]() ii)
ii)
![]() iii)
iii)
![]() iv)
iv)
![]()
Solution
i) 0 since the graph passes through (-3,0) continuously.
ii) Does not exist, since the left hand side approaches 2 and the right hand side approaches (the different value of) -1.
iii) Does not exist, since there is an asymptote on the left hand side there.
iv) -1, since if you fill in the hole you get the point (2,-1).
B) At what points is f(x)
not continuous?
Solution
-1 (a break), 0 (an asymptote), and 2 (a hole).
C) At what points is f(x) not differentiable?
Solution
PROBLEM 4
Evaluate the following limits if they exist.
A)
![]()
Solution
9 - 6 -
3
0
=
9 - 15 +
6
0
We must do algebra
(x + 3)(x -
1)
x - 1
=
(x + 3)(x +
2)
x + 2
Now plug in to get
-4 / -1 = 4
B)
![]()
Solution
Plug in to get
1 +
1
2
=
=
-2/3
1 - 3 -
1
-3
C)
![]()
Plug in to get
x3 - 0 + 0 = x3
PROBLEM 5 The amount of algae in Lake Tahoe over the past twenty years can be modeled by the function
A(t) = 200 e.06t
where t represents the time in years after 1968 and A
represents the kg of algae in the lake.
A) Is
this model a differentiable function? Explain.
Solution
Yes, exponentials are differentiable and multiplying by nonzero constants does not change differentiability.
B) Use a
graphing calculator to graph this function.
Over what domain is this a reasonable model?
Solution
From the problem the domain starts at t = 0 (1968). After fifty years the algae is already over 4,000 kg. With environmental laws as they are, the lake shouldn't get more polluted than this. Other answers are ok, as long as they come with a reasonable explanation.
C) Approximate
(with the assistance of your graph) the slope of the tangent line when t
= 20 and when t = 40.
When t = 20, we use the trace features to get the two points
(19.996154, 663.87019) and (20.004486, 664.20216)
Now find the rise over the run
664.20216 - 663.87019
20.004486 - 19.996154
= 38.84
When t = 40, we use the trace features to get the two points
(39.94195, 2196.97) and (40.07957, 2215.17)
Now find the rise over the run
2215.17
- 2196.97
40.07957
- 39.94195
= 132.25
D) What
do your answers from part C mean in terms of the algae in Lake Tahoe?
We see that the rate of algae growth increases by a factor greater than 3.
PROBLEM 6 Find dy/dx
for the following
![]()
![]()
Solution
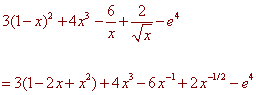
Now we can take the derivatives using the power rule. Notice that e4 is a constant so the derivative of that term is zero. We get
3(-2 + 2x) + 12x2 + 6x-2 - x -3/2
PROBLEM 7 Use the limit definition of the derivative to find the derivative of
![]()
Solution
We have
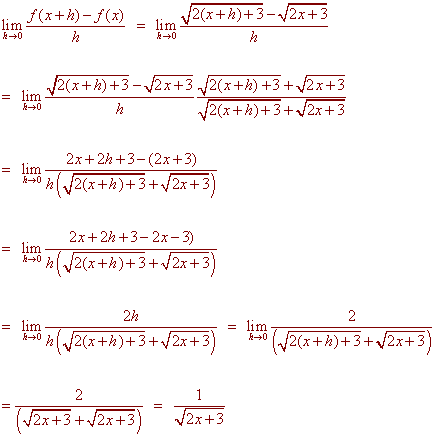
PROBLEM 8 Your research shows that the profit P in dollars from renting out x bicycles at your bicycle rental shop that you manage is given by
P = -.03x2 + 25x - 40
A. Find the additional profit when rentals increase from 25 to 26 units.
Solution
We find
P(26) - P(25) = 589.72 - 566.25 = 23.47
B. Find the marginal profit when x = 25.
We find the derivative at 25:
P'(x) = -.06x + 25
P'(25) = -.06(25) + 25 = 23.5
Extra Credit:
Write
down one thing that your instructor can do to make the class better and one
thing that you think the instructor should not change.
(Any constructive remark will be worth full credit.)