Math 115 Practice Final

Please workout each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Printable Key

Problem 1  Find y' for the following

A.  y  =  x2 (1 - x)5

Solution

B. 

Solution

C.  x3 - 3xy  =  2    at (2,1)

Solution

 

Problem 2  Find the following limits if they exist

A. 

Solution

B. 

Solution

 

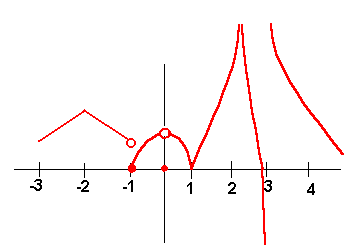
Problem 3  The graph of f(x) is given below.  Find the values of c such that 

A.  does not exist.

Solution

B.  f(x) is not continuous at x  =  c.

Solution

C.  f(x) is not differentiable at x  =  c.

Solution

       

 

 

 

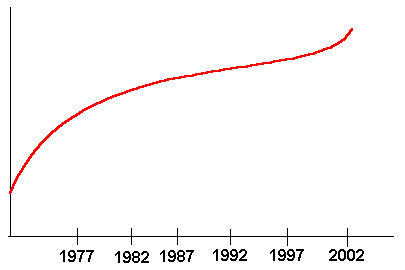
Problem 4  The annual revenue of the Tahoe Eats restaurant is pictured in the figure below.  Visually locate the point of inflection.  Interpret this point in terms of how revenue is increasing or decreasing.  What can you say about the revenue growth of the restaurant over the last thirty years?

       

Solution

 

 

 

 

Problem 5  The concentration C in milligrams per milliliter of a chemical in a patient's bloodstream t hours after injection into a muscle tissue is modeled by

                           3t3
        C  =                                          
                    10 - 10t2 + 9t3

A.  Use differentials to approximate the change in concentration of the chemical when t changes from 1 to 1.1 hour.

Solution

B.  Use your graphing calculator to sketch the graph of the concentration and determine how long it will take until the medicine has the greatest effect.

Solution

C.  Find the horizontal asymptote of the concentration function.  If you were a doctor discussing this medication with your patient, how would you explain the medical implications of the horizontal asymptote?

Solution

 

Problem 6  Without the use of the graphing capabilities of your graphing calculator, determine the relative extrema, inflection points, and asymptotes.  Determine the relative extrema, inflection points, and asymptotes.  Determine the intervals where the graph of the function is increasing and where it is decreasing.  Determine where the graph is concave up and where the graph is concave down.  Then sketch the graph of the function.  

        y  =  3x4 - 8x3 + 6x2 

 Solution

 

Problem 7  The demand function for a haircut is 

        x  =  600 - 2p2 

A.  At what price should a haircut be in order to maximize revenue?

Solution

B.  Determine the elasticity at the price of $12 and interpret your result.

Solution