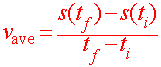Rates of Change

Velocity

Recall that the difference between speed and velocity is that velocity has direction and speed does not.  In other words, the speed is the absolute value of velocity.  We have seen that the secant line can be used to approximate the velocity.  The formula for average velocity is

If we want the instantaneous velocity we take the limit as t_f  approaches t_i.  This is just the alternate form of the derivative.  This leads to the definition below

Example  

The height of a pine cone t seconds after falling from a tree is given by

        s = -16t² + 100

A.   Find the average velocity in the interval [0,2]

B.   Find the instantaneous velocity for t = 0 and t = 1

C.   How long will it take to hit the ground

D.   Find the velocity when it hits the ground

Solution:

A.   We compute 

                      s(b) - s(a)              100 - 36
        v_ave =                          =                          =  32 ft/sec
                          b - a                         2

B.            s'(t) = -32t 

        so 

                s'(0) = 0         and         s'(1) = -32

C.    We solve   

                -16t² + 100 = 0     or      t = 2.5

D.       s'(2.5) = -80

Marginals

In economics the key terms are revenue, cost,  and profit.  We use the word marginal to indicate the additional cost of producing one more.  In calculus terms marginal means the derivative.

Example

Suppose that the cost of producing x burgers per hour is 

        C(x)  =  1000/x + x         for         x > 35

The burgers cost 2.50 each.  Find the marginal cost, marginal revenue, and marginal profit of producing 40 burgers

Solution:  

The marginal cost is 

        C'(x) = (1000x ^-1 + x)' = -1000x ^-2 + 1

so that 

        C'(40) = -1000/1600 + 1 = .375

so that the additional cost of producing 40 burgers is about 38 cents

Revenue is price times number sold

            R  =  2.5x 

so 

            R' =  2.5 

so that the marginal revenue is $2.50.

The profit is 

            Profit  =  Revenue - Cost 

so the marginal profit is 

        marginal revenue - marginal cost 

        =  2.5 - .38  =  2.12

Example

You are the owner of the Tahoe View Inn and have experimented with different pricing strategies.  When you charged $80 per night, you were able to average 50 occupied rooms and when you charged $90 per night, you were able to average 45 occupied rooms.  Find the marginal revenue at an average of 50 occupied rooms assuming the demand function is linear.  Then interpret its meaning.

Solution

We need to first find the demand function.  Since it is linear, we need to find its slope.  We calculate

                      90 - 80
        m  =                          =  -2        
                      45 - 50

Using the point slope formula for the equation of a line gives

        p - 80  =  -2(x - 50)  =  -2x + 100

        p  =  -2x + 180

Since

        Revenue  =  (Price)(Quantity) 

we have

        R(x)  =  (-2x + 180)(x)  =  -2x² + 180x

To find the marginal revenue we calculate

        R'(x)  =  -4x + 180

Now plug in x  =  50 to get 

        R'(50)  =  -4(50) + 180  =  -20

Since the marginal revenue is negative, this says that increasing the occupancy rate will decrease revenue at a rate of $20 per unit.  We should strive to decrease the occupancy rate by raising the price.  Later on, we will learn how to find the price at which the maximal revenue will be achieved.

Back to the calculus home page

Back to the math department home page

e-mail Questions and Suggestions