The Chain Rule


The Chain Rule

Our goal is to differentiate functions such as

        y = (3x + 1)10  


The Chain Rule 

If 
          y = y(u) 

is a function of  u, and 

          u = u(x) 

is a function of x then

           dy           dy        du
                    =                                       
           dx            du       dx         
 


In our example we have

        y  =  u10

and 

        u  =  3x + 1 

so that

        dy/dx  =  (dy/du)(du/dx) 

        =  (10u9) (3)  =  30u9  =  30 (3x+1)9  

 

Proof of the Chain Rule

Recall an alternate definition of the derivative:

       
 

 

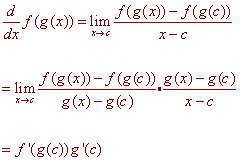
Examples  

Find f '(x) if

  1. f(x) = (x3 - x + 1)20

  2. f(x) = (x4 - 3x3 + x)5

  3. f(x) = (1 - x)9 (1-x2)4

  4.                (x3 + 4x - 3)7
    f(x)  =                               
                      (2x - 1)3 

Solution:

  1. Here 

            f(u) = u20

    and 

            u(x) = x3 - x + 1

    So that the derivative is 

            [20u19] [3x2 - 1]  =  [20(x3 - x + 1)19] [3x2 - 1]

  2. Here 

            f(u) = u5

    and 

            u(x) = x4 - 3x3 + x

    So that the derivative is 

            [5u4] [4x3 - 9x2 + 1]  =  [5(x4 - 3x3 + x)4] [4x3 - 9x2 + 1]

  3. Here we need both the product and the chain rule.  

            f'(x) = [(1 - x)9] [(1 - x2)4]' + [(1 - x)9] '  [(1 - x2)4]

    We first compute

            [(1 - x2)4] ' = [4(1 - x2)3] [-2x]

    and

            [(1 - x)9] '  = [9(1 - x)8] [-1]

    Putting this all together gives

            f'(x) = [(1 - x)9] [4(1 - x2)3] [-2x]  -  [9(1 - x)8]  [(1 - x2)4]

  4. Here we need both the quotient and the chain rule.

                   (2x - 1)3 [(x3 + 4x - 3)7] '  -  (x3 + 4x - 3)7 [(2x - 1)3] '
    f '(x) =                                                                                             
                                                            (2x - 1)6

    We first compute

            [(x3 + 4x - 3)7] ' = [7(x3 + 4x - 3)6] [3x2 + 4]

    and

            [(2x - 1)3] '  = [3(2x - 1)2] [2]

    Putting this all together gives

                           7(2x - 1)3 (x3 + 4x - 3)6 (3x2 + 4)  +  6(x3 + 4x - 3)7 (2x - 1)2
            f '(x) =                                                                                                          
                                                                         (2x - 1)6 



    Exercise

    Find the derivative of 

                        x2(5 - x3)4
        f(x)  =                             
                            3 - x

 

 

Application

Suppose that you put $1000 into a bank at an interest rate r compounded monthly for 3 years.  Then the amount A that will be in the account at the end of the three years will be

A = 1000(1 + r/12)36

Find the rate at which A rises with respect to a rise in the interest rate when the interest rate is 6%.

 

Solution

We are asked to find a derivative.  We use the chain rule with

        u  =  1 + r/12        and        A(u)  =  1000u36 

The two derivatives are

        u'  =  1/12        and        A'  =  36000u35 

The chain rule gives

        dA/dr  =  dA/du du/dr  =  (1/12) 36000 u35

        =  3000 u35  =  3000(1 + r/12)35 

Now plug in   r   =   6%  =  0.06   to get

        3000(1 + 0.06/12)35  =  3572.18

 

Back to the calculus home page

Back to the math department home page

e-mail Questions and Suggestions