Curve Sketching

A List of Interesting features of a Graph

Below is a list of features of a graph that may assist in curve sketching:

  1. x-intercepts

  2. y-intercepts

  3. Domain and Range

  4. Continuity

  5. Vertical Asymptotes

  6. Differentiability

  7. Intervals of Increase and Decrease

  8. Relative Extrema

  9. Concavity

  10. Inflection Points

  11. Horizontal Asymptotes

Most graphs contain only some of these eleven features, so to sketch a graph we find as many interesting features as possible and use these features to sketch the graph.

Examples

Example 1:  

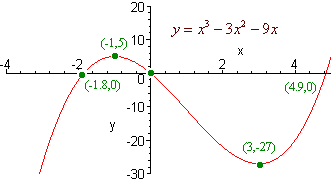
Graph 

y = x3 - 3x2 -9x

  1. We find the x intercepts by factoring out the x and putting into the quadratic formula.

            (-1.8,0), (0,0), (4.9,0)

  2. Note that the y intercept is also (0,0).

  3. The domain is R since this is a polynomial.

  4. The function is continuous since it is a polynomial.

  5. There are no vertical asymptotes since we have a polynomial.

  6. The function is differentiable everywhere.

  7. We find 

            f '(x) = 3x2 - 6x - 9 = 3(x - 3)(x + 1).

    We see that f is increasing on (- ,-1) and on (3, ).  f is decreasing on (-1,3)

  8. By the first derivative test, f has a relative maximum at (-1,5) and a relative minimum at (3,-27).

  9.         f ''(x) = 6x - 6 

    so that f is concave down on (- ,1) and concave up on (1, ).

  10. f(x) has an inflection point at (1,-11).

  11. f has no horizontal asymptotes.

The graph of f is shown below:

 

       

 

 

Example 

Graph 

                        x        
        y =                     
                     x2 - 1

 

Solution:

x-int at (0,0)

Same for y-int

                        (x2 - 1)(1) - x(2x)                 -x2 - 1
        f '(x) =                                        =                          
                                (x2 - 1)2                        (x2 - 1)2

Since the numerator is never zero, so there are no local extrema and f(x) is increasing when x > 1 or x < -1.  Now take the second derivative

       

        

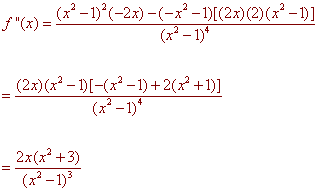
The second derivative is 0 when x = 0 and is positive when x is between - 1 and 0 or x is greater than 1. This is where f(x) is concave up. It is concave down elsewhere except at 0 and 1.

f(x) has a vertical asymptote at x = 1 and -1.

The horizontal asymptote is y = 0.

The graph is shown below.

       

 

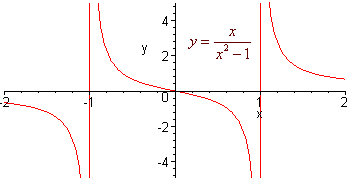
Back to the calculus home page

Back to the math department home page

e-mail Questions and Suggestions