The First Derivative Test
The First Derivative Test (Motivation and Theorem)
If f is a function, then f has a relative maximum at x = c if for all points a near c, f(c) > f(a), and f has a relative minimum at x = c if for all points a near c, f(c) < f(a).
Consider a relative maximum, we have that on the left, the function is increasing and on the right the function is decreasing. Similarly, for a relative minimum, on the right the function is decreasing and on the left the function is increasing.
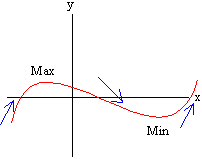
We can now state the first derivative test:
|
Let f be a differentiable function with f '(c) = 0 then
|
Example
Find and classify the relative extrema of
f(x) = x(1 - x)2/5
Solution
First set the first derivative equal to zero to locate the critical points.
f '(x) = (1 - x)
2/5 - 2/5 x(1 - x) -3/5 =
0
Now multiply by (1 - x) 3/5
(1 - x) - 2/5 x = 0,
1 - 7/5 x = 0, x = 5/7 @ 0.714
So there is a critical point at 5/7. Notice
also that there is a critical point at x = 1 since the first
derivative is undefined there (notice the negative exponent -3/5). To determine whether the critical
point is a relative max, min or neither, choose a number just above and just
below the critical value.
| x | 0.7 | 0.8 | 2 |
| f '(x) | 0.04 | -0.3 | 1.8 |
| Result | Increasing | Decreasing | Increasing |
We see that f is increasing to the left of the critical number
and decreasing to the right of the critical number. Hence 5/7 is a
relative maximum.
The actual graph is shown below
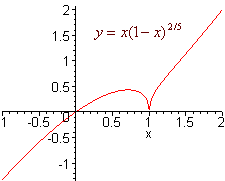
Exercise
Classify the relative extrema of
f(x)= x + 1/x
Answer (Hold your mouse on the yellow rectangle)
![]()
Global Extrema
|
Definition of a Global Extrema We say that a function f has a global maximum (minimum) on [a,b] at c if for all x in [a,b], f(c) > x (f(c) < x) |
To determine the global maximum and minimum we proceed as follows:
1) Find all critical points of f and write down the y values in a table
2) Find f(a) and f(b) and add them to the table.
3) The largest number in the table will be the global maximum, and the smallest number in the table will be the global minimum.
Example
Find the Global Max and Min of
f(x) = 2x3 +3x2 - 36x + 2
on the interval [-10,3]
Solution
We compute
f '(x) = 6x2 + 6x - 36 = 6(x - 2)(x + 3)
Hence there are critical points at 2 and -3.
We compute f(2) = -42, f(-3) = 83, f(-10) = -1942, f(3) = -25
| c | f(c) |
| -10 | -1338 |
| -3 | 83 |
| 2 | -42 |
| 3 | -25 |
Hence on [-10,3], f has a global minimum of -1338 at x = -10 and a global maximum of 83 at x = -3.
Below is the graph.

Exercise:
Find the absolute extrema of
x3 - 12x on the interval [0,4].
Answer (Hold your mouse on the yellow rectangle)
![]()
Application
The cost in cents of supplying x burgers is
C = .5x2 + 100 0 < x < 200
Determine the number of burgers that will minimize the average cost.
Solution
The average cost is given by the Cost divided by the number of units. We have
Ave = C/x = 0.5 x + 200/x
Take a derivative to find the critical points
Ave ' = 0.5 - 200/x2 = 0 Multiply by x2
0.5 x2 - 200 = 0
x2 + 400 = 0
x = 20
Now use a table to determine whether the minimum occurs at the critical point or the endpoint.
| x | Ave |
| 0 | Undefined (infinity) |
| 20 | 20 |
| 200 | 101 |
We can see that supplying 20 burgers will give the minimum average cost of 20 cents per burger.
Back to the calculus home page