Lines and Planes
Lines
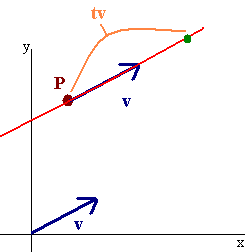
Our goal is to come up with the equation of a line given a vector v parallel
to the line and a point (a,b,c) on the line. The figure
(shown in 2D for simplicity) shows that
if P is a point on the line then
<x,y> = P + tv
for some number t.
The picture is the same for 3D. The formula is given below.
| Parametric Equations of a Line
The parametric equations for
the line through the point (a,b,c)
and parallel to the vector v
are |
Example:
Find the parametric equations of the line that passes
through the point (1, 2, 3) and is parallel to the vector
<4, -2, 1>
Solution:
We write:
<x, y, z> = <1, 2, 3> + t
<4, -2, 1> = <1 + 4t, 2 - 2t, 3 +
t>
or
x(t) = 1 + 4t, y(t) = 2 - 2t,
z(t) = 3 + t
Exercise
Find the parametric equations of the line through
the two points (2,1,7) and (1,3,5).
Hint: a vector parallel to the line has tail at (2,1,7)
and head at (1,3,5).
If S is a plane then a vector n is normal (perpendicular) to the plane if
it is orthogonal to every vector that lies on the plane. Suppose that
n is a normal vector to a plane and (a,b,c) is a point on the plane. Let
(x,y,z) be a general point on the plane, then
<x - a, y - b, z - c> 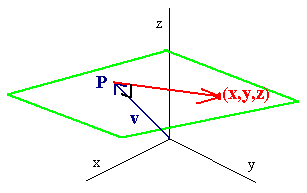
is parallel to the plane, hence
| n . <x - a, y - b, z - c> = 0 |
this defines the equation of the plane.
Example:
Find the equation of the plane that contains the
point (2,1,0) and has normal vector <1,2,3>
Solution:
We have
<1,2,3> . <x -
2,y - 1,z - 0> = 0
so that
1(x - 2) + 2(y - 1) + 3z =
0
or
x + 2y + 3z = 4
Example
Find the equation of the plane through the points
P =
(0,0,1) Q = (2,1,0)
and R = (1,1,1)
Solution
Let
v =
Q - P = <2, 1, -1>
and
w = R - P = <1,
1, 0>
then to find
a vector normal to the plane, we find the cross product of v and
w:
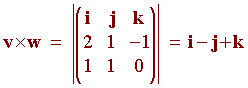
or
<1, -1, 1>
We can now use the formula:
<1, -1,
1> . <x, y, z - 1> = 0
or
x - y + z - 1 = 0
or
x - y + z = 1
Distance Between a Point and a Plane
Let P be a point and Q be a point on a plane with normal vector n, then the
distance between P and the plane is given by
|
Distance Between a Point P and a Plane With Normal Vector n Let Q be a point on the plane with normal vector n. The the distance from the point P to this plane is given by
||PQ . n|| |
Example 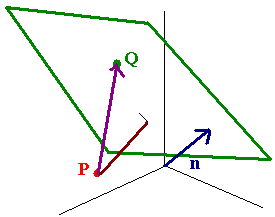
Find the distance between the point (1,2,3) and the
plane
2x - y - 2z = 5
Solution
The normal vector can be read off from the equation as
n = <2, -1, -2>
Now find a convenient point on the plane such as Q = (0, -5, 0). We have
PQ = <-1, -7, -3>
and
n . PQ = -2 + 7 + 6 = 11
We find the magnitude of n by taking the square root of the sum of the squares. The sum is
4 + 1 + 4 = 9
so
|| n || = 3
Hence the distance from the point to the plane is 11/3.
The Angle Between 2 Planes
The angle between two planes is given by the angle between the normal vectors.
Example
Find the angle between the two planes
3x - 2y + 5z = 1
and 4x + 2y - z
= 4
We have the two normal vectors are
n = <3,-2,5>
and m = <4,2,-1>
We have
n . m =
3,
![]()
hence the angle is
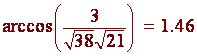
Back to the Math 107 Home Page