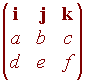The Dot and Cross Product

The Dot Product

                 Definition
We define the dot product of two vectors

     v = ai + bj  and w = ci + dj 

to be

          v . w = ac + bd 


Notice that the dot product of two vectors is a number and not a vector.  For 3 dimensional vectors, we define the dot product similarly:

Dot Product in R3 

If 

     v = ai + bj + ck and w = di + ej + fk

then 
          v . w = ad + be + cf

 

 

Examples:

If 

        v  =  2i + 4j  

and 

        w  =  i + 5j

then

        v . w  =  (2)(1) + (4)(5)  =  22

 

Exercise

Find the dot product of 

        2i + j - k     and     i + 2j

The Angle Between Two Vectors

We define the angle theta between two vectors v and w by the formula

                            v . w           
        cos q  =                  
                         ||v|| ||w|| 

so that
        

v . w = ||v|| ||w|| cos q


Two vectors are called orthogonal if their angle is a right angle.  

We see that angles are orthogonal if and only if 

        v . w  =  0

Example  

To find the angle between 

        v =  2i + 3j + k 

and 

        w  =  4i + j + 2k 

we compute:

       
and

       

and

        v . w  =  8 + 3 + 2 = 13

Hence 
 

       

 

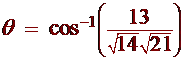
Direction Angles



     Definition of Direction Cosines

Let 

          v = ai + bj + ck  

be a vector, then we define the direction cosines to be the following:

  1.                   a
    cos a  =           
                     ||v||

  2.                   b
    cos b  =           
                     ||v||

  3.                   c
    cos g  =           
                     ||v||

 

Projections and Components Suppose that a car is stopped on a steep hill, and let g be the force of gravity acting on it.  We can split the vector g into the component that is pushing the car down the road and the component that is pushing the car onto the road.  We define

                   Definition

 Let u and v be a vectors.  Then u can be broken up into two components, r and s such that r is parallel to v and s is perpendicular to v.  r is called the projection of u onto v and s is called the component of u perpendicular to v.  

We see that 

                                                   ||u|| ||v|| ||projvu ||   
        u . v  =  ||u|| ||v|| cos q   =                                    
                                                           ||u||


                                          =  ||v|| ||projvu ||

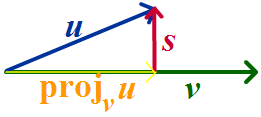
Vectors u,v,s, proj_v u

hence 

                        u . v
  ||projvu ||  =                 
                         ||v||


We can calculate the projection of u onto v by the formula:          

                  u . v
projvu =                v 
                   ||v||2 

 Notice that this works since if we take magnitudes of both sides we get that

                        u . v
|    |projvu|| =                ||v|| 
                         ||v||2 

and the right hand side simplifies to the formula above.  The direction is correct since the right hand side of the formula is a constant multiple of v so the projection vector is in the direction of v as required.

To find the vector s, notice from the diagram that

projvu + s = u

so that

s  =  u - projv u

Work

The work done by a constant force F along PQ is given by 

W = F . PQ 

 

Example

Find the work done against gravity to move a 10 kg baby from the point (2,3) to the point (5,7)? 

Solution

We have that the force vector is 

        F  =  ma  =  (10)(-9.8j)  =  -98j

and the displacement vector is

        v  =  (5 - 2) i  +  (7 - 3) j  =  3i + 4j

The work is the dot product

        W  =  F . v  =  (-98j) . (3i + 4j)  

        =  (0)(3) + (-98)(4)  =  -392

Notice the negative sign verifies that the work is done against gravity.  Hence, it takes 392 J of work to move the baby.

 

Torque

Suppose you are skiing and have a terrible fall.  Your body spins around and you ski stays in place (do not try this at home).  With proper bindings your bindings will release and your ski will come off.  The bindings recognize that a force has been applied.  This force is called torque.  To compute it we use the cross produce of two vectors which not only gives the torque, but also produces the direction that is perpendicular to both the force and the direction of the leg.

The Cross Product Between Two Vectors


                          Definition  
Let u = ai + bj + ck  and v = di + ej + fk be vectors then we define the cross product v x w by the determinant of the matrix:

                                

We can compute this determinant as

       

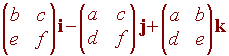
        =  (bf - ce) i + (cd - af) j + (ae - bd) k

Example

Find the cross product u x v if

        u  =  2i + j - 3k            v  =  4j + 5k

 

Solution

We calculate

       

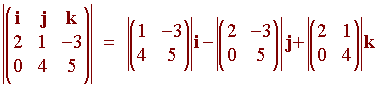
        =  17i - 10j + 8k

        

If you need more help see the lecture notes for Math 103 B on matrices.

Exercises

Find u x v when

  1. u = 3i + j - 2k,      v = i - k

  2. u = 2i - 4j - k,      v = 3i -  j + 2k

Notice that since switching the order of two rows of a determinant changes the sign of the determinant, we have

         u x v  =  -v x u

Geometry and the Cross Product

Let u and v be vectors and consider the parallelogram that the two vectors make.  Then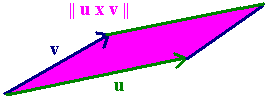

        ||u x v|| = Area of the Parallelogram

and the direction of u x v is a right angle to the parallelogram that follows the right hand rule 

Note:   For i x j the magnitude is 1 and the direction is k, hence i x j = k.

 

Exercise

Find j x k and i x k

Torque Revisited

We define the torque (or the moment M of a force F about a point Q) as

M = PQ x F

 

Example

A 20 inch wrench is at an angle of 30 degrees with the ground.  A force of 40 pounds that makes and angle of 45 degrees with the wrench turns the wrench.  Find the torque.

Solution  

We can write the wrench as the vector

        20 cos 30  i  +  20 sin 30  j  = 17.3 i  +  10 j

and the force as

        -40 cos 75 i - 40 sin 75 j = -10.3 i - 38.6 j

hence, the torque is the magnitude of their cross product:

       

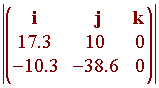
        =  -564 inch pounds

Parallelepipeds

To find the volume of the parallelepiped spanned by three vectors u, v, and w, we find the triple product:

Volume = u . (v x w)

This can be found by computing the determinate of the three vectors:

   

 

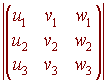
Example

Find the volume of the parallelepiped spanned by the vectors

        u  =  <1,0,2>        v  =  <0,2,3>        w  =  <0,1,3>

Solution

We find

      

 

Back to the Vector Page

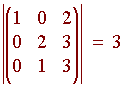
Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions