Locating and Classifying Local Extrema

I.  Quiz

II.  Homework

III.  Definition of Relative Max and Min

A function f(x,y) has a relative maximum at (a,b) if there is a delta neighborhood centered at (a,b) such that

f(a,b) > f(x,y)

similarly there is a relative minimum at (x,y) if

f(a,b) < f(x,y)

for all (x,y) in the delta neighborhood.  

Theorem:  If f(x,y) has a relative maximum or minimum then gradf = 0 there.

A visual proof will be given in class.

Example   Let f(x,y) = x² + xy - 2y + x - 1

then gradf = <2x + y + 1,x - 2> = 0

so that x - 2 = 0 or x = 2

Hence 2(2) + y + 1 = 0  so y = 5

A possible extrema is (2,-5)

Theorem (Second Derivative Test For Functions of Two Variables)

We call the matrix:  

fxx	fxy
fyx	fyy

the hessian then the determinant is  

D = f_xxf_yy - f_xy² 

then if gradf = 0 we have the following

D	fxx	Type
>0	>0	Rel Min
>0	<0	Rel Max
<0	any	Saddle
= 0	any	Test Fails

We will discus saddle points in class

Example:

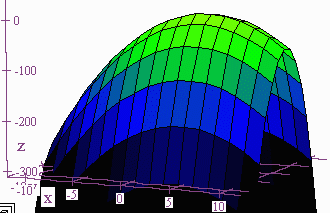
Let f(x,y) = -x² - 5y² + 8x - 10y - 13   

then gradf = <-2x + 8,-10y - 10> = 0 at (4,-1)

we have f_xx = -2,  f_yy = -10, and f_xy = 0 Hence

D = (-2)(-10) - 0 > 0

so f has a relative maximum at (4,-1)

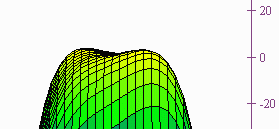
Example:  Let

f(x,y) = 4xy - x⁴ - y⁴

The gradf = <4y - 4x³,4x - 4y³>

We solve:

4y - 4x³ = 0 so that y = x³  

Hence 4x - 4(x³)³ = 0

x - x⁹ = 0 so that x = 1 or x = 0 or x = -1

this gives us the points (1,1), (0,0) and (-1,-1)

We have f_xx = -12x²,  f_yy = -12y², and f_xy =  4

Hence D = 144x²y² - 16

We write the table:

Point	D	fxx	Type
(1,1)	126	-12	Max
(0,0)	-16	0	Saddle
(-1,-1)	126	-12	Max

IV.  Minimizing Distance

Find the minimum distance from the point (2,1,4) to the plane

x + 2y + z = 5

Solution:  We minimize the square of the distance:

D = (x - 2)² + (y - 1)² + (5 - x - 2y - 4)²

We take thr gradient and set it equal to 0:

<2(x - 2) - 2(5 - x - 2y - 4),2(y - 1) - 2(5 - x - 2y - 4)> = 0

so

2x - 4 - 10 + 2x + 4y + 8 = 0  and 2y - 2 - 10 + 2x + 4y + 8 =  0

4x + 4y - 6 = 0 and 2x + 6y - 4 = 0

2x + 2y - 3 = 0 and 2x + 6y - 4 = 0

subtracting the first from the second, we get:

4y - 1 = 0 so y = 1/4

Hence x = 7/4

Finally, we have

D = (7/4 - 2)² + (1/4 - 1)² + (5 - 7/4- 2(1/4) - 4)²

V.  The Least Squares Regression Line

Example:

Suppose you have three points in the plane and wnat to find the line y = mx + b that is closest to the points. Then we wnat to minimize the sum of the squares of the distances, that is find m and b such that

d₁² + d₂² + d₃² is minimum

We calculate

d₁² + d₂² + d₃²  = f = (y₁ - (mx₁+ b))² + (y₂ - (mx₂+ b))² + (y₃ - (mx₃+ b))²  

To minimize we set

gradf = <f_m, f_b> = 0  (Notice that m and b are the variables)

f_m = 2(y₁ - (mx₁+ b))(-x₁) + 2(y₂ - (mx₂+ b))(-x₂) + 2(y₃ - (mx₃+ b))(-x₃) = 0

f_b = -2(y₁ - (mx₁+ b)) - 2(y₂ - (mx₂+ b)) - 2(y₃ - (mx₃+ b)) = 0   

We have

A)  x₁(y₁ - (mx₁+ b)) + x₂(y₂ - (mx₂+ b)) + x₃(y₃ - (mx₃+ b)) = 0    

B)   (y₁ - (mx₁+ b)) + (y₂ - (mx₂+ b)) + (y₃ - (mx₃+ b)) = 0 

In sigma notation, we have

A)  sum x_iy_i - m sum x_i² - b sum x_i = 0

B)  sum y_i - m sum x_i - nb = 0 where n = 3

We can solve to get

m = [n  sum x_iy_i - sum x_i  sum y_i ]/[n sum x_i²  - (sum x_i)²]

and b = 1/n( sum y_i - msum x_i )

Exercise:  Find the equation of the regression line for

(3,2), (5,1) and (4,3)