Limits

I.  Quiz

II.  Homework

III.  Topology Terminology

Let P be a point in the plane then a delta neighborhood (ball) of P is the set of points that are less than delta units away from P.  If R is a region, then a point P is called an interior point of R if there is a delta neighborhood totally contained in R.  If every point of R is an interior point of R then R is called open. A point P is called a boundary point of R if every delta neighborhood of R contains both points in R and not in R.  R is called closed if it contains all of its boundary points.

IV.  The Definition of a Limit

Let f(x,y) be a function defined near the point P, then lim  x -> P f(x,y) = L if there is a delta such that f(x,y) is close to L for all points (except possibly P) in the delta neighborhood of P.  Equivalently, the limit is L if all path that lead to P, the function also tends towards P.  (Recall that for the one variable case we needed to check only the path from the left and from the right.) To show that a limit does not exist at a point we need only find two paths that both lead to P such that f(x,y) tends towards different values.

V.  Techniques For Finding Limits.

Example:

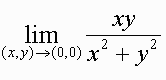
Solution:  First select the path along the x-axis.  On this path y = 0 so the function becomes:

f(x,0) = 0/x² = 0

Now choose the path along the y = x line:

f(x,x) = x²/(2x²) = 1/2

Hence the function tends towards two different values for different paths.

Example:   Find

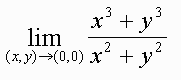
We could try the paths from the last example, but both paths give a function value of 0 for the limit.  Hence we suspect that the limit exists.  We convert to polar coordinates and take the limit as r -> 0:

We have f(r,theta) =  (r³cos³ theta + r³sin³ theta)/r²  = rcos³ theta + rsin³ theta

as r -> 0 the function also -> 0 no matter what theta is.  Hence the limit is 0.

Exercises:  Find the limit if it exists

 A.  lim (x,y) -> (0,1) of (xy - x)/(x² + y² - 2y + 1)

B.  lim (x,y) -> (4x²y²)/(x⁴ + y⁴)

VI.  Continuity

We define a function of several variables to be continuous at a point P if the limit exists at P and the function defined at P is equal to this limit.  

As with functions of one variable, polynomials are continuous, sums, products, and compositions of continuous functions are continuous.  Quotients of continuous functions are continuous.  A function is continuous if it is continuous at every point.