Differentials

I.  Quiz

II.  Homework

III.  The Total Differential

Definition:  Let z = f(x,y) then the total differential for z is

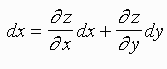
Example:  For z = f(x,y) = x² + xy

dz = (2x + y)dx + xdy

Exercise:  Find dz if z = xsinycosy

IV.  Application

In Chemistry we learn that PV = NRT, where NR is a constant.  We can write:

T = PV/NR = kPV

Suppose at 25 degrees C gas is in an expanding cylinder of 55cc at a pressure of 3 atm.  Also suppose that the pressure is increased by .1 atm and the volume is decreased by .05 cc.  Then

dT = kPdV + kVdP approx k[(3)(-.05) + 50(.1)) = .35k

so that there is an increase on the temperature of  about k(.35) degrees c

V.  Error

Suppose that you measured the dimensions of a tin can bo be

h = 6 +- .1 inch and

r = 2 +- .05 inch

What is the approximate error in your measurement for the volume of the can?

Solution:

We have V = pi r²h  

Hence the error can be approximated by

= 1.2 pi + .4 pi = 1.6 pi approx 5.0 cu inches

Hence the volume is

V = 75.4 +- 5 cu inches

VI.  Differentiability

Theorem: If a function f(x,y) is differentiable at a point (a,b) then it is continuous at (a,b)

where differentiable means

Delta f(x,y) = f_x(a,b)delta x + f_y(a,b)deltay + e₁deltax + e₂deltay

where both e₁ and e₂ approach 0 as delta x and delta y approach 0.  Furthermore if the partial derivatives are continuous then the function is differentiable.