Vector Algebra
I. Quiz
II. Homework
III. Algebra of Vectors
If v = <a,b> and w = <c,d> and k is a constant, then
v + w = <a + c,b + d>
kv = <ka,kb>
Example
3<2,1> - 2<-1,3> = <6 + 2,3 - 3> = <8,0> = 8i
Geometrically v+w is the vector that corresponds to the diagonal of the parallelogram with two sides v and w.
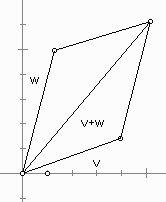
The appropriate diagram will be drawn to show how v-w = v + (-w).
IV. Properties of Vector Addition and Subtraction
We have the following four properties of vectors: If u, v ,and w are vectors and a and b are numbers then
1) (u + v) + w = u + (v + w)
2) a(u + v) = au + av
3) a(bv) = (ab)v
4) u + v = v + u