Lines and Planes
I. Quiz
II. Homework
III. Lines
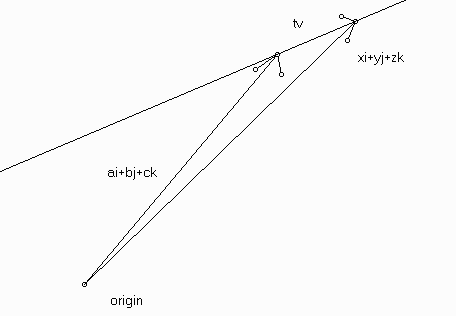
Our goal is to come up with the equation of a line given a vector v parallel to the line and a point (a,b,c) on the line. The figure shows that if (x,y,z) is a point on the line then <x,y,z> = <a,b,c> + tv for some number t.
Example: find the parametric equations of the line that passes through the point (1,2,3) and is parallel to the vector <4,-2,1>
We write:
<x, y, z> = <1,2,3> + t<4,-2,1> = <1 + 4t,2 - 2t,3 + t> or
x(t) = 1 + 4t, y(t) = 2 - 2t, z(t) = 3 + t
Exercise: find the parametric equations of the line through the two points (2,1,7) and (1,3,5).
Hint: (a vector parallel to the line has tail at (2,1,7) and head at (1,3,5))
IV. Planes
If S is a plane then a vector n is normal (perpendicular) to the plane if it is orthogonal to every vector that lies on the plane. Suppose that n is a normal vector to a plane and (a,b,c) is a point on the plane. Let (x,y,z) be a general point on the plane, then <x - a, y - b, z - c> is parallel to the plane, hence
n @ <x - a, y - b, z - c> = 0
this defines the equation of the plane.
Example: Find the equation of the plane that contains the point (2,1,0) and has normal vector <1,2,3>
Solution:
We have
<1,2,3>@<x - 2,y- 1,z - 0> = 0
1(x - 2) + 2(y - 1) + 3z = 0
x + 2y + 3z = 4
Example: find the equation of the plane through the points P = (0,0,1), Q = (2,1,0) and R = (1,1,1)
Solution:
Let v = Q - P = <2,1,-1> and w = R - P = <1,1,0> then a to find a vector normal to the plane, we find the cross product of v and w:
v x w =
| i | j | k |
| 2 | 1 | -1 |
| 1 | 1 | 0 |
i - j + k or <1,-1,1>
We can now use the formula:
<1,-1,1>@<x,y,z - 1> = 0
x - y + z - 1 = 0
x - y + z = 1
V. Distance Between a Point and a Plane
Let P be a point and Q be a point on a plane with normal vector n, then the distance between P and the plane is given by
ProjnPQ = ||PQ@n||/||n||
A picture will be given
Exercise: find the distance between the point (1,2,3) and the plane 3x - y + 4z = 5
VI. The Angle Between 2 Planes
The angle between two planes is given by the angle between the normal vectors.
Example: Find the angle between the two planes 3x - 2y + 5z = 1 and 4x + 2y - z = 4
We have n = <3,-2,5> and m = <4,2,-1>
n@m = 3, ||n|| = sqrt(39) and ||m||= sqrt(21) hence the angle is
arccos(3/[sqrt(39)sqrt(21)]