Alternating Series

I.  Quiz

II.  Homework

III.  The Alternating Series Test

Suppose that a weight from a spring is released.  Let a₁ be the distance that the spring drops on the first bounce.  Let a₂ be the amount the weight travels up the first time.  Let a₃  be the amount the weight travels on the way down for the second trip. Let a₄ be the amount that the weight travels on the way up for the second trip, etc.

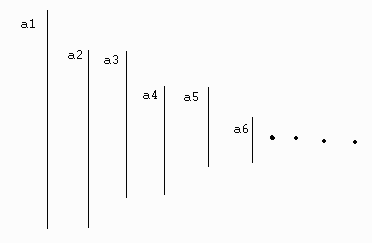
Then  eventually the weight will come to rest somewhere in the middle. This leads us to

Theorem: The Alternating Series Test   

Let a_n > 0 for n and suppose that the following two conditions hold:

1) { a_n } is a decreasing sequence for large n.

2)

Then the corresponding series sum (-1)ⁿa_n  converges.

Proof:  

We have

s_2n = (a₁ - a₂) + (a₃ - a₄) + ...+ (a_2n-1 - a_2n) > 0

and

s_2n = a₁ - (a₂ - a₃) - (a₄ - a₅) - ...- (a_2n-2 - a_2n-1) - a_2n   

So  s_2n < a₁  

Hence s_2n  is bounded and monotonic and hence converges.  Since s_2n+1 -> s_2n  the limit of the partial sums exist and hence the series converges.

IV.  Examples     

sum of (-1)ⁿ /n converges since the limit of 1/n is 0 and 1/n > 1/(n + 1)

Exercises:  

Determine whether the following converge:

A)  Sum (-1)^{n + 1}/n!

B)  Sum (-1)ⁿ n²/(n + 1) 

V.  The Remainder Theorem

Consider the spring example again.  The weight will always be between the two previous positions.  Hence we have

The Remainder Theorem

Let L = sum (-1)ⁿa_n   then

|L - s_n| < a_{n + 1}   

Example:  Use a calculator to determine

sum (-1)ⁿ⁺¹/n

With an error of less than .01

Solution:

We have Error < .01 so choose n such that a/n < .01 (n = 101)

Then use your calculator.

VI.  Absolute and Conditional Convergence

Definitions:  

1)  sum(-1)ⁿa_n  is called absolutely convergent if sum a_n converges

2)  sum (-1)ⁿa_n   is called conditionally convergent if sum(-1)ⁿa_n  converges, but sum a_n  diverges.

For example the alternating harmonic series  is conditionally convergent sum (-1)ⁿ⁺¹/n

while the series sum (-1)ⁿ⁺¹/n² is absolutely convergent. 

VII.  The Rearrangement Theorem:  Let sum (-1)ⁿ⁺¹a_n be a conditionally convergent series and let k be a real number.  Then there exists a rearrangement of the terms so that you add them up and end up with k. As strange as it may seem, addition is not commutative for conditionally convergent series.  On the other hand for absolutely convergent series any rearrangement produces the same limit.