Surfaces
Let C be a curve, then we define a cylinder to be the set of
all lines through C and perpendicular to the plane that
C lies in.
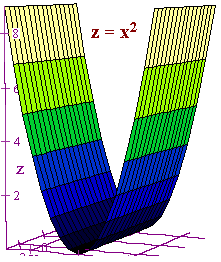
We can tell that an equation is a cylinder is it is missing one of the
variables.
Quadric Surfaces
Recall that the quadrics or conics are lines , hyperbolas,
parabolas, circles, and ellipses. In three dimensions, we can combine
any two of these and make a quadric surface. For example
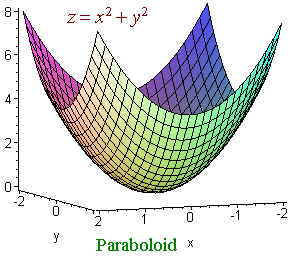
is a paraboloid since for constant
z we get a circle and for
constant x or y we get a parabola. We use the suffix -oid to mean ellipse
or circle. We have:
-
x2 y2 z2
a2 b2 c2
-
x2 y2 z2
-
a2 b2 c2
-
x2 y2 z2
a2 b2 c2
Surface of Revolution
Let y = f(x) be a curve, then the equation of the surface
of revolution abut the x-axis is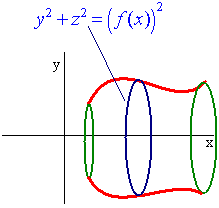
y2 + z2 = f(x)2
Example
Find the equation of the surface that is formed when the curve
y = sin x 0 < x < p/2
is revolved around the y-axis.
Solution
This uses a
different formula since this time the curve is revolved around the y-axis.
The circular cross section has radius sin-1 y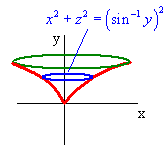 and the circle is perpendicular to the y-axis. Hence the equation is
and the circle is perpendicular to the y-axis. Hence the equation is
x2 + z2 = (sin-1 y)2
Cylindrical Coordinates
We can extend polar coordinates to three dimensions by
|
x = rcosq |
Example
We can write (1,1,3)
in cylindrical coordinates. We find
![]()
and
![]()
so
that the cylindrical coordinates are
(![]() ,
p/4, 3)
,
p/4, 3)
Spherical Coordinates
An alternate coordinate system works on a distance and two
angle method called spherical coordinates. We let r
denote the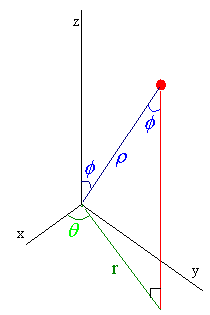 distance from the point to the origin, q represent the same
q as in
cylindrical coordinates, and f denote the angle from the positive z-axis
to the point. The picture tells us that
distance from the point to the origin, q represent the same
q as in
cylindrical coordinates, and f denote the angle from the positive z-axis
to the point. The picture tells us that
r = r sin f
and that
z = r cos f
From this we can find
|
x = rcosq =
r sin f cosq |
Immediately we see that
x2 + y2 + z2
=
r2
We use spherical coordinates whenever the problem involves a distance from a source.
Example
convert the surface
z = x2 + y2
to an equation in spherical coordinates.
Solution
We add z2 to both sides
z + z2 = x2 + y2 + z2
Now it is easier to convert
r cos f + r2 cos2 f = r2
Divide by r to get
cos f + r cos2 f = r
Now solve for r.
cos f
cos f
r
=
=
= csc f cot f
1 - cos2 f
sin2 f
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions