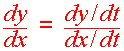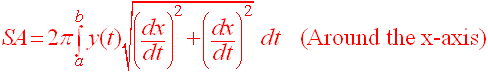Tangent Lines
The Derivative of Parametric Equations
Suppose that
x = x(t)
and y
= y(t)
then
as long as dx/dt is nonzero
|
|
Example:
Find dy/dx for
x(t) =
2 cos t and y(t)
= 2 sin t
Solution:
We have
dx/dt =
-2 sin t and dy/dt
= 2 cos t
hence
dy dy /
dt
=
dx
dx / dt
2 cos t
=
= -cot t
-2 sin t
The Second Derivative of Parametric Equations
To calculate the second derivative we use the chain rule twice.
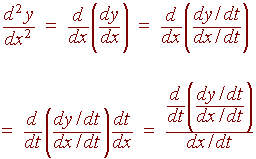
Hence to find the second derivative, we find the derivative with respect to t of the first derivative and then divide by the derivative of x with respect to t.
Example
Let
x(t) = t3
y(t) = t4
then
dy 4t3
4
=
= t
dx
3t2 3
Hence
d2y
d/dt (4/3 t)
4/3 4
=
=
=
dx2
dx / dt
3t2
9t2
Arc Length
We can find the arc length of a curve by cutting it up into tiny pieces and adding up the length of each of the pieces. If the pieces are small and the curve is differentiable then each piece will be approximately linear.
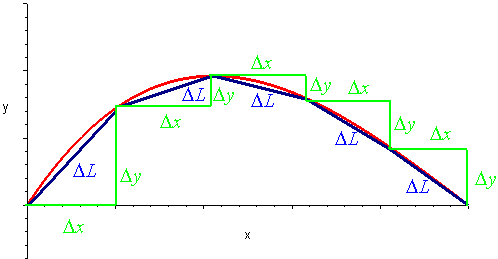
We can use the distance formula to find the length of each
piece
![]()
Multiplying and dividing by D gives
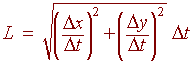
Adding up all the lengths and taking the limit as Dt
approaches 0 gives the formula
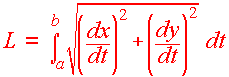
|
Example
Find the arc length of the curve defined parametrically by
x(t) = t2 + 4t,
y(t) = 1 -
t2, 0 < t < 2
Solution
We calculate
x ' = 2t + 4,
y ' = -2t
Hence
![]()
The integral of this
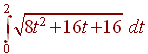
Is quite difficult (but not impossible) to do by hand. Either by hand or by computer we get
12.74
Surface Area of Revolution
If we revolve a curve around the x-axis what is surface area of the
region that is formed? If we cut the curve into tiny pieces, then each
piece is approximately a line segment, which when revolved around the x-axis
will have area
2p (radius)
(length) = 2p y(t)
![]() Dt
Dt
Similarly, if the piece of the curve is revolved about the y-axis, then the
resulting surface are is
2p (radius)
(length) = 2p x(t)
![]() Dt
Dt
Adding up all the pieces and taking the limit as Dt
approaches 0 gives
Definition of Surface Area 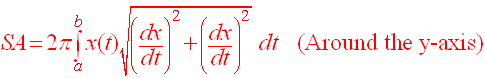
|
Example
Set up the integral that gives the surface area of the solid formed by revolving the curve
x(t) = t2 , y(t) = t3
About the y-axis
Solution
We compute
x' = 2t, y' = 3t2
The formula gives
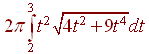
Back to the Polar and Parametric Equations Page
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions