Parametric Equations
Lines
Recall that a line has equation
y = mx + b
Suppose that one airplane
moves along the line
y
= 2x + 3
while the other airplane moves along the
line
y
= 3x - 2
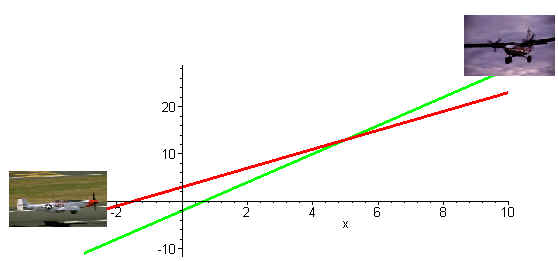
Can you tell whether the airplanes collide? Even
though the lines intersect, the equations themselves do not tell us whether
there will be a mid air collision. To be able to mathematically model
this scenario, we use parametric equation. We introduce the variable
t for time and write x and y as a function of
t.
Consider the two sets of equations:
-
x(t) = t, y(t) = 2t + 1
-
x(t) = 2t, y(t) = 4t + 1
These describe the same line, but the second one travels twice as fast.
Definition
|
Finding the Parametric Equations for a Line Given Two Points
Example:
Find the parametric equations for the line through
the points (3,2) and (4,6) so that when t = 0 we are at the point
(3,2) and
when t = 1 we are at the point (4,6).
Solution:
We write symbolically:
(x,y) = (1 - t) (3, 2)+
(t) (4, 6)
= (3 - 3t + 4t, 2 - 2t + 6t)
= (3 + t, 2 + 4t)
so that
x(t) =
3 + t
and y(t)
= 2 + 4t
If y = f(x) is a function of x we can write parametric equations by writing
x =
t and y
= f(t).
Example
The parabola
y = x2
can be
represented by the parametric equations:
x =
t
and y
= t2
Consider the circle centered at (0,0) with radius 2. We can write it
parametrically as
x(t) =
2cos(t)
and y
= 2sin(t)
We see that the circle is drawn in a counterclockwise direction. We can draw the same circle as
x(t) =
2cos(-t)
and y(t)
= 2sin(-t)
now the circle is drawn clockwise. We can also write
x(t) =
2 cos(t2)
and y = 2 sin(t2)
now the circle begins slowly and speeds up.
A Cool Example
The graph of
x(t) = 11cost - 6cos(11/6 t)
and y(t) = 11sin(t) - 6sin(11/6
t)
is pictured below:
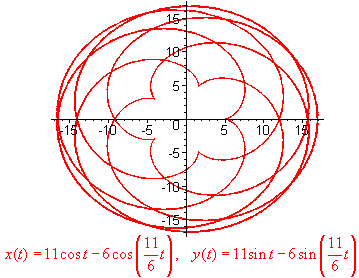
Eliminating the Parameter
If a curve is given by parametric equations, we often are interested in
finding an equation for the curve in standard form:
y =
f(x)
Example
Consider the parametric equations
x(t) = t2
and y(t) =
sin(t) for t >
0
To find the conventional form of the equation we solve for t:
t =
![]()
hence
y = sin(![]() )
)
is the equation.
Example
Eliminate the parameter for
x(t) =
et
and y(t) = e2t + 1
Solution
We write:
y(t) = (et)2 + 1
Hence
y = x2 + 1
Let
x1(t)
= 2t + 1
and y1(t)
= 4t2
and
x2(t)
= 3t and
y2(t) = 3t
Do they intersect? If so then there is a c with
2c + 1 = 3c
and
4c2 = 3c
the first equation gives us that
c = 1
Putting this into the second equation
we have
4 = 3
which tells us that they do not intersect. Do their graphs intersect?
If so then there exists a c and a k such that
2c + 1 = 3k
and
4c2 = 3k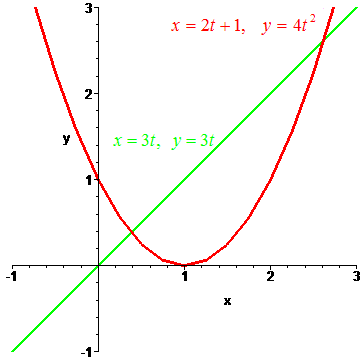
Hence, we see that
2c + 1 = 4c2
or that
4c2 - 2c - 1 =
0
We solve to get two intersection points
![]()
hence their graphs intercept. Their graphs are shown on the right.
Back to the Polar and Parametric Equations Page
Back to the Math 107 Home Page