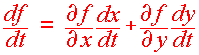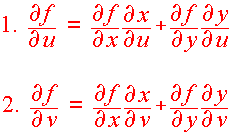The Chain Rule
Review Of The Chain Rule For One Variable
Recall that if
y =
f(x) and x
= x(t)
then
dy dy
dx
=
dt
dx dt
Example
Suppose that
z = f(x,y) =
x2 + 2x - xy + y2
and
x(t) = t2
+1
y(t) = t3 - t2
Then what is dz/dt for t = 2?
Solution:
f can be written as
[x(t)]2 + 2[x(t)] -
x(t)y(t) + [y(t)]2
Hence the derivative is
2x(t)[x'(t)] + 2(2t) - [x(t)y'(t) +
y(t)x'(t)] + 2y(t)y'(t)
= 2x(t)[2t] + 2(2t) - [x(t)(3t2 - 2t) + y(t)(2t)] + 2y(t)(3t2
-
2t)
Now since t = 2,
x(2) =
5 and
y(2) = 4
We can substitute in to get
2(5)[2(2)] + 2(2)(2) -
[(5)(3(2)2- 2(2)) + (4)2(2))] + 2(4)(3(2)2- 2(2))
= 56
Alternatively we use the chain rule:
|
A Chain Rule
|
With this chain rule the derivative becomes
(2x + 2 - y)(2t) + (-x + 2y)(3t2 - 2t)
When
t = 2,
x(2) = 5
and
y(2)
= 8 - 4 = 4
hence
df / dt = [2(5) + 2 - 4](2)(2) + [-5 +
2(4)] [3(4) - 2(2)] = 56
Exercise:
Let
f(x,y) = 2x -3xy
and
x(q)
= 2 cos q and
y(q) = 2 sin q
Find df/dq
The Chain Rule for 2 Variables
|
A Chain Rule For Two Variables Let f(x,y) be a 2 variable function and x = x(u,v) and y = y(u,v) then
|
Example: Polar Coordinates
Let
f(x,y) = x2y
and
x = r cos q
and y = r sin q
then
![]()
= 2xy cos q +
x2 sin q
= 2r2 cos2
q
sin q +
r2cos2 q sin q
= 3r2cos2q sinq
Exercise
Let
f(x,y) = x - 2y2
and
x(u,v) = u -
2v
y(u,v) = 2u + v
find
![]()
Implicit Differentiation
Suppose we have the ellipsoid
x2 + y2 + 2z2
= 1
and we want to find
![]()
We write
f(x,y,z) = f(x, y, z(x,y))
= 0
but
![]()
Where the first factors correspond to the partials with respect to the first,
second and third variables respectively and the second factors are with respect
to the actual x. We have
Jx/Jx = 1
and Jy/Jx = 0
Hence
0 = Jf/Jx +
Jf/Jz Jz/Jx
So that
Jz/Jx =
-Jf/Jx / Jf/Jz =
-fx/fz
for the ellipsoid:
Jf/Jx = 2x/4z =
x/2z
In
general,
| zx = -fx/fz and zy = -fy/fz |
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page