Partial Fractions
The Fundamental Theorem of Algebra
The fundamental theorem of algebra states that if P(x) is a polynomial of
degree n then P(x) can be factored into linear factors over the complex numbers.
Furthermore, P(x) can be factored over the real numbers as a product
of linear and quadratic terms and any rational function can be split up as
a sum of rational function with denominators of the form
(x -
r)n
or
x2 + Ax +
B
Partial Factions
Example
Consider the rational function
3x +
2
3x +2
P(x) =
=
x2 -
1
(x - 1)(x + 1)
We want to write it in the form
3x +
2
A
B
=
+
(x - 1)(x +
1)
x - 1 x + 1
To do this we need to solve for A and B. Multiplying by the common denominator
(x - 1)(x + 1)
we have
3x + 2 = A(x + 1) + B(x - 1)
Now let x = 1
5 = 2A + 0
A = 5/2
Now let x = -1
-1 = -2B
B = 1/2
Hence we can write
3x +
2
5/2
1/2
=
+
x2
-
1
x - 1 x
+ 1
This is called the partial fraction decomposition of P(x)
Example 2
Find the Partial Fraction Decomposition of
3x2 + 4x +
7
3x2 + 4x + 7
P(x) =
=
x3 - 2x2 +
x
x(x-1)2
We write
3x2 + 4x +
7
A
B
C
=
+
+
x(x-1)2
x - 1 (x -
1)2
x
Multiplying by the common denominator, we have
A(x)(x - 1) + Bx + C(x - 1)2 = 3x2 + 4x + 7
Let x = 0:
C = 7
Let x = 1:
We have
B = 14
Now look at the highest degree coefficient:
Ax2 + Cx2 = 3x2
Dividing by x2 and substituting C = 7
A + 7 = 3, A = - 4
We conclude that
3x2 + 4x +
7
-
4
14
7
=
+
+
x(x-1)2
x - 1 (x -
1)2
x
Integration
Example: Evaluate
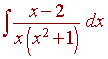
We write
x2 -
2
A
Bx +
C
=
+
x(x2 +1)
x
x2 + 1
Multiplying by the common denominator, we have
A(x2 + 1) + (Bx + C)x = x2 - 2
Let x = 0
A = -2
Hence
(Bx + C)x = x2 - 2 + 2x2 + 2 = 3x2
So that
Bx2 + Cx = 3x2
We see that B = 3 and C = 0
Hence

Exercise
Find
![]()
Logistics Growth
It has been said that the total population of South Lake Tahoe should
never exceed 30,000 people. If in 1980 the population was
15,000 and
in 2000 it was 20,000, when will the population reach
25,000?
Solution:
We make the assumption that the rate of increase of
the population is proportional to the product of the current population and
30,000 minus the current population. That is:
dP
= kP(30,000 - P)
dt
This is a separable differential equation. Separating gives
dP
= kdt
P(30,000 - P)
Now integrate both sides. The right hand side is
kt + C
To
integrate the right hand side, use partial fractions:
1
A
B
=
+
P(30,000 -
P)
P
30,000 - P
Multiplying by the common
denominator:
1 = A(30,000 - P) + BP
P = 0:
1 = 30,000A or A = 1/30,000
P = 30,000: 1 = 30,000B
or B = 1/30,000
Now integrate to get
1
1
lnP -
ln(30,000 - P) = kt + C
30,000
30,000
or
P
ln
= at + b
30,000 - P
When t = 0, P = 15,000, so
b = 0
When t = 20, P = 20,000, so
20a = ln2
or
ln 2
a =
20
hence
P
t ln 2
ln =
30,000 -
P
20
Finally
t ln 2
ln 5 =
20
or
20 ln 5
t =
= 46.4
ln 2
The population will reach 2500 in the year 2026.
Partial Fractions Exercises
Exercises
A.
![]()
B .
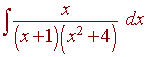
C.
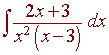
D.
![]()
Back to Techniques of Integration Page