Separable Differential Equations

 

A differential equation is called separable if it can be written as

f(y)dy = g(x)dx

To solve a separable differential equation

  1. Get all the y's on the left hand side of the equation and all of the x's on the right hand side.

  2. Integrate both sides.

  3. Plug in the given values to find the constant of integration (C)

  4. Solve for y

Example:

Solve dy/dx = y(3 - x);   y(0 )= 5

  1. dy/y = (3 - x) dx

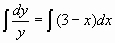  2. ,  lny = 3x - x2 + C

  3. ln5 = 0 + 0 + C,  C = ln5

  4. y = exp(3x - x2 + ln5) = exp(3x - x2)exp(ln5) = 5exp(3x - x2)

Exercises:  

A)  dy/dx = x/y;   y(0) = 1    B)  dy/dx = x(x+1);  y(1) = 1    C)  2xy + dy/dx = x;  y(0) = 2

 

A differential equation is called a homogeneous differential equation if it can be written in the form 

M(x,y)dx + N(x,y)dy = 0

where M and N are of the same degree.  To solve a homogeneous differential equation

  1. Rewrite the differential in homogeneous form  M(x,y)dx + N(x,y)dy = 0

  2. Make the substitution y = vx where v is a variable. 

  3. Then use the product rule to get
    dy = vdx + xdv

  4. Substitute to rewrite the differential equation in terms of v and x only

  5. Divide by xd   where d is the degree of the polynomials M and N.

  6. Follow the steps for solving separable differential equations.

  7. Resubstitute v = y/x.

Example
Solve y' = (x + y)/(x - y)

Solution

  1. dy/dx = (x + y)/(x - y)        (x + y)dx + (y - x)dy  =  0

  2. y = vx

  3. dy = vdx + xdv

  4. (x + vx)dx + (vx - x)(vdx + xdv) = 0

  5. (1 + v)dx + (v - 1)(vdx + xdv) = 0

  6. [(1 + v) + (v2 - v)]dx + (xv - x)dv = 0        [1 + v2]dx  =  (x - xv)dv
    1/x dx = (1 - v)/(1 + v2)dv = 1/(1 + v2)dv -  v/(1 + v2)dv

  7. At this point of the class, we do not know the integral of 1/(1 + v2).  In a later section, we will see that an antiderivative is arctan(v), hence
    ln|x| = arctan(v) - 1/2 ln(1 + v2) + C

  8. ln|x| = arctan(y/x) - 1/2 ln(1 + (y/x)2) + C