NAME                                   

MATH 106 PRACTICE MIDTERM 2

 

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

 

PROBLEM 1  Set up the integrals that solve the following problems.  Sketch the appropriate diagram for each.  Then use a calculator to finish the problem.

A)   (10 Points) Find the volume of the solid that is formed by revolving the region bounded by y  =  x3 + x and y  =  x2 + x  around the y-axis.
Solution

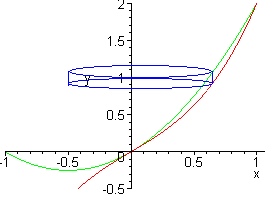
We choose a vertical cross-section since we do not want to solve for y.  The picture shows that this produces a cylinder.  The Surface area of a cylinder is

        A  =  2prh
        r  =  x
        h  =  (x2 + x) - (x3 + x)  =  x2 - x3

To find the limits, we set the equations equal to each other:

        x2 + x  =  x3 + x

        x2  =  x2 

              x  =  0    or     x  =  1

We get the integral

          =  .3142 

B)    (10 Points). Find the volume of the solid that is formed by revolving the region bounded by  y  =  x4  and y  =  x between x  =  0 and  x  =  1/2  about the line y  =  -10.

Solution

 

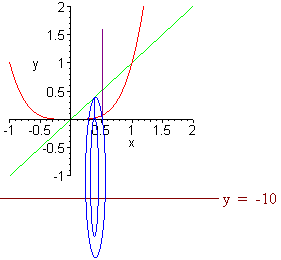
We choose a vertical cross-section again since we do not want to solve for y.  The picture shows that this produces a washer.  The area of a washer is

        A  =  p(R2 - r2)
        R  =  x + 10
        r  =  x4 + 10

We get the integral

          =   7.59

C)   (10 Points) Find the volume of the solid that is formed by revolving the region bounded by y  =  x3 - x  and y  =  3x around the line x  =  5.
Solution

         

 

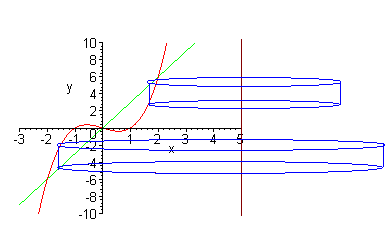
From the picture, we can see that since the top curve changes we will need to perform two integrations.  We can also see that we will need to use the method of cylindrical shells.  The Surface area of the bottom cylinder is

        A  =  2prh
        r  =  5 - x
        h  =  (x3 - x) - (3x)  =  x3 - 4x

The Surface area of the top cylinder is

        A  =  2prh
        r  =  5 - x
        h  =  3x - (x3 - x)  =  4x - x3 

To find the limits, we set the equations equal to each other:

        x3 - x  =  3x

        x3 - 4x   =  0 

        x(x - 2)(x + 2)

              x  =  -2    or     x  =  0    or    x  =  2


We get the integral

       

           =   80p

D)   (10 Points) Find the area of the region bounded by the curves
        y  =  x3 - 3x2 - 9x + 12 and y  =  x + 12

Solution

 

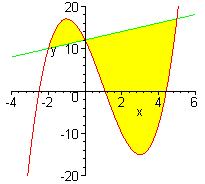
Notice that there are two regions.  We set

         x3 - 3x2 - 9x + 12  =  x + 12

         x3 - 3x2 - 10x  =  0

        x(x - 5)(x + 2)  =  0

        x  =  -2    or    x  =  0    or    x  =  5

We integrate

   =  101.75
        

E)    (10 Points) Find the length of the curve y  =  sin x for  0 <   x  < 2p.

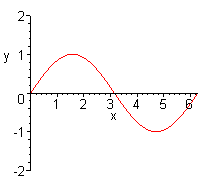
We use the arc length formula:

        1 + y'2  =  1 + cos2 x

So that the length is

       

F)    (10 Points) Find the volume of the sphere of radius 2.

Solution

   

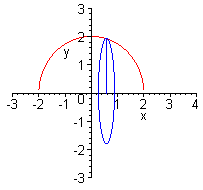
We can find the volume of the sphere by revolving the curve

       

about the x-axis.  The picture shows that we can use the disc method with

         A  =  pr2

         r2  =  4 - x2
We get the integral

                 

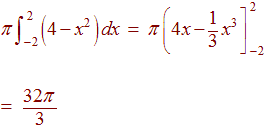
PROBLEM 2

A)   (10 Points)   Find the derivative of sec-1(2x + 1)

Solution

Use the chain rule

       

        

B)    (10 Points) Show that      

Solution

       

 

 

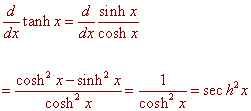
PROBLEM 3 Find the following indefinite integrals

A)   (15 Points)  

Solution

Let 

        u  =  4 - x2     du  =  -2x dx

 

B)    (15 Points)

Solution

We first complete the square   

        x2 + 2x + 10  =  x2 + 2x + 1 - 1 + 10

        =  (x + 1)2 + 9

Now integrate

       

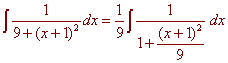
        u2  =  (x + 1)2 / 9        u  =  (x + 1) / 3        du  =  1/3 dx

We get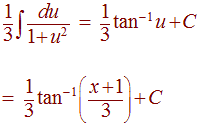

       

 

 

Problem 4   (20 Points)

When completed, the International Space Station orbiting at 238 miles above the surface of the earth will weigh one million pounds (at the surface of the earth 4000 miles from the center).  How much total work will it take to send the entire station in orbit?

  Solution

We use the fact that 

        F  =  k / x2

           1,000,000  =  k / 40002 

        k  =  1.6 x 1013     

So that 

       

 

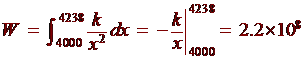
It will take 220 million mile pounds to send the entire station in orbit.

Problem 5  (20 Points)

A 30 foot chain that weighs 3 pounds per foot is used to lift a 200 pound piece of sheet metal from the ground to the top of a 30 foot tall building.  How much work is required?

Solution

We have

        Work  =  Work for the sheet metal + Work for the chain

Work for the sheet metal  =  (200)(30)  =  6,000

To find the work for the chain, we have

        DW  =  (3Dy)(30 - y)

The total work is the integral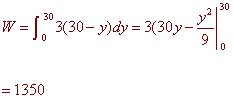

       

The total work is 

        6000 + 1350  =  7350 foot pounds

 

Back to the Math Department Home Page

Questions, Comments and Suggestions:  Email:  greenl@ltcc.edu