Name                                    

 

MATH 106 PRACTICE MIDTERM 1

 

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

     Printable Key

 

 PROBLEM 1  Please answer the following true or false.  If false, explain why or provide a counter example.  If true, explain why or state the proper theorem.

A)  Suppose that f(x) and g(x) are differentiable inverse functions, and f '(2) = 3.  Then g'(2) = 1/3.

     Solution

       False. It would be true if we said that g'(f(2)) =  1/3.

 

 

B)   If f is a differentiable function such that both f and f ' are positive for all x, then g(x)  =  ln(f(x)) is increasing for all values of x.

    Solution

True,  since 

                           f '(x)
        g '(x)  =                      
                            f(x)

is positive if both f ' and f are positive

PROBLEM 2  Calculate the derivatives of the following functions.

A)            d
                       (2x)1-x
               dx

     Solution

        (2x)1-x  =  e(1 - x)ln(2x)

Now use the chain and product rules.  The derivative of 

        (1 - x)ln(2x) 

is 

        (1 - x)(1/x) - ln(2x)  =  1/x - 1 - ln(2x)

Hence the derivative of 

         e(1 - x)ln(2x)

is 

        [1/x - 1 - ln(2x)](2x)1-x

 

B)        d
                     eln(sin x)
            dx

     Solution

First use the inverse property of e and ln to get

        eln(sin x)  =  sin x

Now the derivative is simply 

        cos x

    

C)         d         23t
                                     
             dx        t

     Solution

We use the quotient rule to get

          t(23t)' -23t
                            
            t2

Now use the chain rule and the fact that 

        bx '  =  bx ln b

to get

          3t ln2 (23t) - 23t
                                       
                     t2


D)      d
                 [ arcsin(1-3x) - (ln x)(arctan x)]
         dx

Solution

We use the chain rule for the first part and the product rule for the second part to get

       

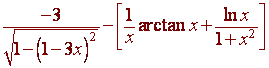
PROBLEM 3 Find the following integrals

A)      

     Solution

Let 

        u  =  1 - x    du  =  - dx        x  = 1 - u

The substitution produces

       

 

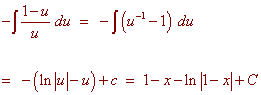
B)    

    Solution 

Let 

        u  =  2 - 3x    du  =  -3 dx

The substitution produces

       

 

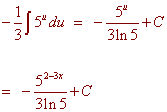
C)      
    Solution

Let 

        u  =  4 - x2     du  =  -2x dx

         

 

D)     


    Solution  

We first complete the square   

        x2 + 2x + 10  =  x2 + 2x + 1 - 1 + 10

        =  (x + 1)2 + 9

Now integrate

       

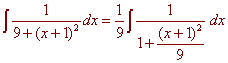
        u2  =  (x + 1)2 / 9        u  =  (x + 1) / 3        du  =  1/3 dx

We get

       

 

 

 

 

 

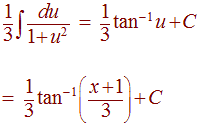
PROBLEM 4    Let  f(x) = 2x3 + 4x + 5

A.  Prove that f(x) has an inverse.
     Solution

We calculate 

        f '(x)  =  6x2 + 4

which is always positive, hence f(x) has an inverse.



B.    Find       d
                             f -1(11)
                     dx
     Solution  

  Solution

We use the inverse formula

             d                                     1
                      f -1(11)   =                                  
             dx                              f '(f -1(11))

Since 

        f(1)  =  11

We have

        f -1(11)  =  1

and 

        f '(1)  =  6(1)2 + 4  =  10

Hence 

            d                                     1                         1
                      f -1(11)   =                                  =               
             dx                              f '(f -1(11))                10

 

PROBLEM 5   

Show that

          d
                     tanh x   =   sech2 x
         dx

     Solution

       

 

 

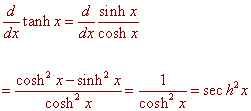
Extra Credit:  Write down one thing that your instructor can do to make the class better and one thing that you do not want changed with the class. 

 

Back to the Math Department Home Page

Questions, Comments and Suggestions:  Email:  greenl@ltcc.edu