Name
MATH 106 PRACTICE
MIDTERM 1
Please work out each of the given
problems. Credit will be based on
the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Please answer the following true or false. If false, explain why or provide a counter example. If true, explain why or state the proper theorem.
A) (10
points) The differential equation
![]() is a homogeneous differential
equation
is a homogeneous differential
equation
True, dividing
numerator by y2 gives
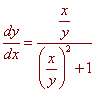
which is a function of x/y.
B) (10 points)
If f is a differentiable function
such that both f and f
' are positive for all x, then g(x) =
ln(f(x))
is increasing for all values of x.
True, since
f '(x)
g '(x)
=
f(x)
is positive if both f ' and f are positive
PROBLEM 2 Calculate the derivatives of the following functions.
A) (10
points)
d
(2x)1-x
dx
(2x)1-x = e(1 - x)ln(2x)
Now use the chain and product rules. The derivative of
(1 - x)ln(2x)
is
(1 - x)(1/x) - ln(2x) = 1/x - 1 - ln(2x)
Hence the derivative of
e(1 - x)ln(2x)
is
[1/x - 1 - ln(2x)](2x)1-x
B) (10
points)
d
eln(sin
x)
dx
First use the inverse property of e and ln to get
eln(sin x) = sin x
Now the derivative is simply
cos x
C) (10
points)
d 23t
dt t
We use the quotient rule to get
t(23t)' -23t
t2
Now use the chain rule and the fact that
bx ' = bx ln b
to get
3t ln2 (23t) - 23t
t2
PROBLEM 3 Find the following integrals
A) (10
points)
![]()
Let
u = 1 - x du = -x dx x = 1 - u
The substitution produces
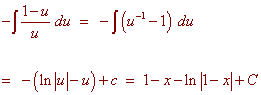
B) (10
points)
![]()
Let
u = 2 - 3x du = -3 dx
The substitution produces
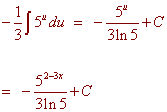
PROBLEM 4 You have been called as an expert witness in the case involving the recent murder that occurred in room E106. It is clear that at the time of death the victim was healthy with a temperature of 98.6 degrees. It is also know that a human body in this situation will cool down to 90 degrees in one hour. When the body was discovered at 10:00 PM the corpse had a body temperature of 85 degrees. During the entire day, the temperature of the room was a constant 65 degrees.
A)
(10 points) Use the Newton’s Law of Cooling (the rate of change of the
temperature of the body is proportional to the difference between the body’s
temperature and the ambient temperature) to write down a differential equation
for this situation.
dT
= k(T - 65), T(0) =
98.6, T(1) = 90
dt
B) (10 points) Solve the differential equation from part A.
Separating variables gives
dT
= kdt
T - 65
Now integrate
ln|T - 65| = kt + C
Now use T(0) = 98.6
ln(98.6 - 65) = C
Now use T(1) = 90
ln|90 - 65| = k + ln(65)
Solving gives
k = ln(25/33.6)
Exponentiating the solution produces
T - 65 = 33.6 eln(25/33.6)t
C) (10 points) What was the time of death?
The body temperature is 85 degrees, hence
Now solve for t
ln(20) - ln33.6
t =
= 1.75476
ln(25/33.6)
Now convert 0.75476 to minutes by multiplying by 60 to get that the murder occurred one hour and 45 minutes ago or at 8:15 PM.
PROBLEM 5 Let f(x) = 2x3 + 4x + 5
- (10 Points) Prove
that f(x) has an inverse.
Solution
We calculate
f '(x) = 6x2 + 4
which is always positive, hence f(x) has an inverse.
- (10 Points) Find
d
dx
We use the inverse formula
d
1
f -1(11)
=
dx
f '(f -1(11))
Since
f(1) = 11
We have
f -1(11) = 1
and
f '(1) = 6(1)2 + 4 = 10
Hence
d
1
1
f -1(11)
=
=
dx
f '(f -1(11))
10
PROBLEM 6 Solve the following differential equations
A. (15 Points)
y(1 + x2)y' - x(1 + y2) =
0, y(0) = ![]()
Solving for dy/dx gives
dy
x(1 + y2)
=
dx
y(1 + x2)
Separating variables gives
y dy
x dx
=
1 + y2
1 + x2
Integrating both sides yields
ln(1 + y2) = ln(1 + x2) + C
The initial value
y(0) = ![]() gives
gives
ln 4 = C
Using the sum to product property of ln gives
ln(1 + y2) = ln(4 + 4x2)
Exponentiating both sides produces
1 + y2 = 4 + 4x2
or
![]()
B. (15 Points)
x3
+ y3
y' =
xy2
This is a homogeneous differential equation. We can write
1 + (y/x)3
y' =
(y/x)2
Letting
v = y/x, y = xv, y' = v + xv'
gives
1
+ v3
v + xv' =
v2
or
x dv
1
=
dx
v2
Separating gives
dx
v2 dv
=
x
Integrating both sides gives
1/3 v3 = ln|x| + C1
Multiplying by 3, letting C = 3C1, and taking the 1/3 power produces
v = (3ln|x| + C)13
Substituting v = y/x and multiplying by x gives
y = x(3ln|x| + C)1/3