Discs and Washers
Volumes of Revolution
Suppose you wanted to make a clay vase. It is made by shaping the clay
into a curve and spinning it along an axis. If we want to determine how
much water it will hold, we can consider the cross sections that are
perpendicular to the axis of rotation, and add up all the volumes of the small
cross sections. We have the following definition:
|
|
where A(x) is the area the cross section at a point
x.
Example: Disks
Find the volume of the solid that is produced when the region bounded by the
curve
y = x2,
y = 0, and
x = 2 
is revolved around the x-axis.
Solution:
Since we are revolving around the x-axis, we have that the cross section is in
the shape of a disk with radius equal to the y-coordinate of the point.
Hence
A(x) = pr2
= p[x2]2
We have
![]()
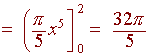
Example: Washers
Find the volume of the solid formed be revolving the region between the
curves
y = x2 and
y =
![]()
about the x-axis.
Solution
We draw the picture and revolve a cross section about the x-axis and come up
with a washer. The area of the Washer is equal to the area of the outer
disk minus the area of the inner disk.
|
A = p(R2 - r2) |
We have that R is the y-coordinate of the top curve ()
and r is the y-coordinate of the bottom curve
(x2). We have
A = p([![]() ]2
- [x2]2) =
p[x - x4]
]2
- [x2]2) =
p[x - x4]
Hence
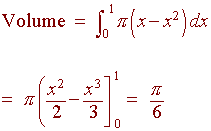
Example: Revolving about the y-axis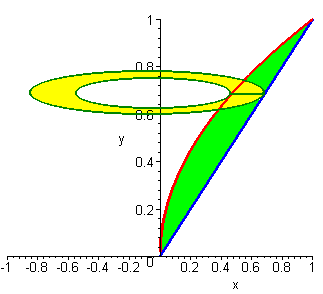
Find the volume of the solid that is formed by revolving the
curve bounded by
y = x
and
y
= ![]()
about the y-axis. This time our cross section is perpendicular to the
y-axis. When we revolve, we get a washer with
R equal to the x-coordinate of the y =
![]() curve
and r equal to the x-coordinate of the y =
x curve. Hence
curve
and r equal to the x-coordinate of the y =
x curve. Hence
A = p((y)2 - (y2)2) = p(y2 - y4)
We get
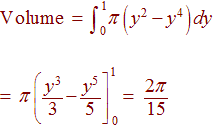
Revolving About a Non-axis Line
Find the volume of the region formed by revolving the curve
y =
x3 0 <
x < 2 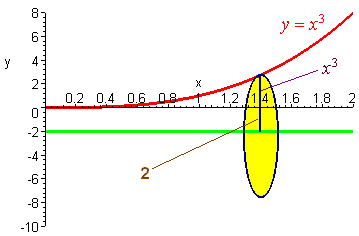
about the line y = -2.
Solution:
This time we revolve the cross-section and
obtain a disk. The radius of the disk is 2 plus the
y coordinate of the
curve. Hence
A = p(2 + x3)2
so that
![]()
This integral can be evaluated by FOILing out the binomial and then integrating each monomial. We get a value of approximately 133.
Example: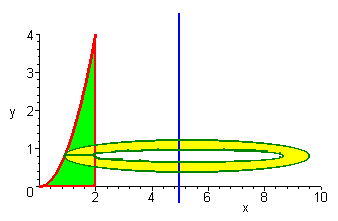
Try revolving the curve
y = x2
from 0 to
2
about the
line x = 5
We have
A = p[(5 -
![]() )2 - 9]
)2 - 9]
so that
![]()
This integral works out to be approximately 59.
Applications of Volume
Example: The Volume of the Khufu Pyramid
The base of the Khufu pyramid is a square with wide length 736 feet and the angle that the base makes with the ground is 50.8597 degrees. Find the volume of the Khufu pyramid.
Solution:
First note that we need to change to
radian measure.
50.8597 degrees = .88767 radians.
The height of the pyramid is
736 tan(.88767) = 904.348
We have that the area of a cross section is s2 where s is the side length of the square.
Placing the y-axis through the top of the pyramid and the origin
at the middle of the base, we have that
s =
![]() x
x
Hence
A(x) = 2x2
Since the axis perpendicular
to the cross sections is the y-axis, we need A in terms of
y.
We set up similar triangles:
x/736 = y/904.348
x = .8138y
Hence
A(y) = 1.3247x2
We calculate
![]()
= 361131 cubic feet.
Example: Volume of a Sphere
A sphere is formed by rotation the curve
![]()
We have
Volume =
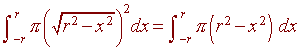
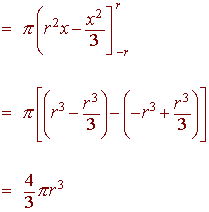
Exercise:
Two cylinders of radius r intersect each
other at right angles. Find the volume of their intersection.
Hint: Consider cross sections parallel to both axes
of rotation. These cross sections are squares. Then show that the
side length is ![]()
Click here for the cored sphere
Back to the Math Department Home
e-mail Questions and Suggestions