Integration by Parts
Derivation of Integration by Parts
Recall the product rule:
(uv)' = u'v + uv'
or
uv' = (uv)' - u'v
Integrating both sides, we have that
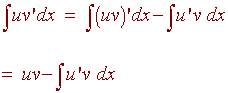
|
Theorem: Integration by Parts Let u and v be differentiable functions, then
|
Examples
A) ![]()
| u = x | du = dx |
| dv = ex dx | v = ex |
Hence we have
![]()
= xex - ex + C
Exercise
Evaluate
![]()
Integration By Parts Twice
Example
Solve
![]()
| u = x2 | du = 2xdx |
| dv = ex dx | v = ex |
We have
![]()
We just did this integral in the last example, so our solution is
x2ex - 2[xex
- ex] + C
The By Parts Trick
Example
Evaluate
![]()
| u = ex | du = ex dx |
| dv = sinx dx | v = -cosx |
We have
![]()
Now try integration by parts again:
| u = ex | du = ex dx |
| dv = cosx dx | v = sinx |
![]()
It seems as if we are back to where we started, however with a clever move, the
answer appears.
Let
![]()
Then we have
I = -excosx + ex sinx - I
Adding I to both sides we get
2I = -excosx + ex sinx
So that
-excosx + ex sinx
I =
+ C
2
We can conclude that
![]()
Other By Parts
Example:
![]()
| u = arctanx |
1 du = 1 + x2 |
| dv = dx | v = x |
We get
![]()
letting
u = 1 + x2, du =
2x dx, x dx = du/2
![]()
Exercise:
Evaluate
![]()
When to Use Integration By Parts
-
When there is a mix of two types of functions such as trig and exponentials, poly and trig, etc.
-
Strange functions such as arctrig and ln.
-
When all else fails.
Back to Techniques of Integration Page