Slope Fields and Euler's Method

Solutions to Differential Equations

A differential equation is an equation that contains derivatives.  We call y = f(x) a solution to a differential equation if plugging in f(x), f '(x), f ''(x), etc. into the differential equation results in a true equality. 

Example

Which of the following is a solution to the differential equation

        y' - 3y  =  0

a.  y = e3x       b.  y  =  2ex        c.  5e3x

Solution

a.   We find y' = 3e3x.  Now plug in y and y' into the differential equation:

        3e3x - 3e3x  =  0

Since this is a true statement, y = e3x is a solution to the differential equation.

b.   We find y' = 2ex.  Now plug in y and y' into the differential equation:

        2ex - 3(2ex)  =  -4ex

Since this is not equal to zero,  y = 2e3x is not a solution to the differential equation.

c.   We find y' = 15e3x.  Now plug in y and y' into the differential equation:

        15e3x - 3(5e3x)  =  0

Since this is a true statement, y = 5e3x is a solution to the differential equation.

We call a differential equation an initial value problem if a the value of y or any of the derivatives of y are given for a specific value of the independent variable.

Example

Given that the general solution to the differential equation

        y' + y/x2 = 0

is

        y  =  Ce1/x

Find the solution to the initial value problem

      

        y' + y/x2 = 0         y(1) = 4

Solution

We just plug in 1 for x and 4 for y into  the general solution

        4  =  Ce1/1 = Ce

Multiplying both sides by e-1 gives

        C  =  4e-1

So that the solution is

        y  =  4e-1e1/x

Slope Fields

There is a graphical representation of a differential equation that can assist us with understanding the solution even if we do not know the algebraic expression of the solution.  This representation is called a slope field.  For a first order (only the first derivative appears in the equation) differential equation, we can write it in the form

        y'  =  f(x,y)

For example, the differential equation

        xy' - y = 4

can be written in the form

                      y + 4
        y'  =                         
                         x

Given any point (x,y) we can use this to find the slope of our solution at that point.  For the above example, the slope of the solution at the point (3,2) is

                      2 + 4
        y'  =                   =  2
                         3

 

We can think of the slope of the direction of the flow at that point.  From the point (3,2), we can draw a small line segment with slope 2.  The applet below by Andy Bennett from
Kansas State University shows some slope fields.  Note that multiplication must be explicitly shown with a "*" such as y' = 2*x*y and not y' = 2xy.

 

It is great to use a computer, but sometimes one is required to sketch a slope field by hand.  To do this we use a version of a T-table and then use small line segments to make the sketch.

Example

Sketch a few representative slopes of the slope field

        y'  =  x - y/2

 

Solution

We will sketch the integer points for -2 < x < 2 and -2 < y < 2.

 
Point (-2,-2) (-2,-1) (-2,0) (-2,1) (-2,2)
Slope -1 -1.5 -2 -2.5 -3
Point (-1,-2) (-1,-1) (-1,0) (-1,1) (-1,2)
Slope 0 -0.5 -1 -1.5 -2
Point (0,-2) (0,-1) (0,0) (0,1) (0,2)
Slope 1 0.5 0 -0.5 -1
Point (1,-2) (1,-1) (1,0) (1,1) (1,2)
Slope 2 1.5 1 0.5 0
Point (2,-2) (2,-1) (2,0) (2,1) (2,2)
Slope 3 2.5 2 1.5 1

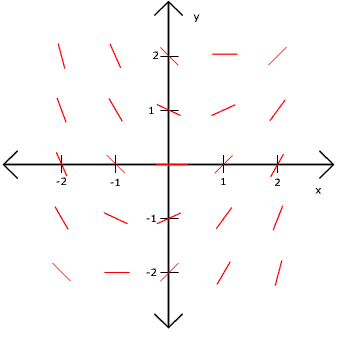
We now draw the slope field by plotting the small line segments centered at the given point with the given slope.  The slope field is shown below.

Euler's Method

The slope field gives us a visual feel for the solutions to a differential equation.  If we start at a point, then we can "follow the flow lines" and come up with a curve.  This is essentially Euler's Method.  Euler's Method tells us to pick a point and a step size.  From the chosen point, move along the flow line a horizontal distance equal to the step size and a vertical distance according to the flow line in order to arrive at a new point.  Next use the new point as the chosen point and move along flow line from this new chosen point.  If we continue this process, we will have a series of points that are approximately on the curve that defines the solution to the differential equation.  Hence if (x0,y0) is the chosen point and h is the step size and y' = f(x,y)is the differential equation, we proceed as follows:

Let

        x1  =  x0 + h

The slope of the tangent line through the point will be

        m = y' = f(x0,y0)

and the equation will be

        y - y0  =  f(x0,y0)(x - x0)

Plugging in x0 + h for x, gives

        y1  =  y0 + h f(x0,y0)

This is how we find the next point.

 

Example

Use Euler's Method to approximate the solution to the differential equation

        y'  =  x - y2     y(2) = 0

with step size h = 0.5.  Find the first four points.

 

Solution

We begin with the given point (2,0).

        f(2,0)  =  2 - 02  =  2

so that

        y1  =  0 + 0.5(2)  =  1

and

        x1  =  2 + 0.5  =  2.5

Now we find the next point.  We have

        f(2.5,1)  =  2.5 - (1)2  =  1.5

Hence

        y2  =  1 + (0.5)(1.5)  =  8.5

and

        x2  =  2.5 + 0.5  =  3

Finally, we find the fourth point.  We have

        f(3,1)  =  3 - (8.5)2  =  -69.25

Hence

        y2  =  8.5 - (0.5)(69.25)  =  -26.625

and

        x2  =  3.0 + 0.5  =  3.5

Hence the first four points from Euler's method are

        (2,0), (2.5,1), (3,8.5), and (3.5,26.625)