Derivatives of the Trigonometric Functions

I.  Quiz

II.  Homework

III.  sin(x)/x

Theorem:  lim h ->0 sin(h)/h = 1

Proof: Consider the diagram below

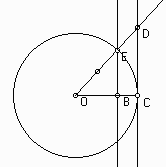
Where the circle is the unit circle.  Then the coordinates of E are (cos(t),sin(t)).  Notice that the the areas have the following orders:

triangle OBE < sector OCE < triangle OCD

Area of OBE = 1/2 sin(t)cos(t), Area of OCE = 1/2 t , Area of OCD = 1/2sin(t)/cos(t)

(since similar triangles give CD = EB/OB = sin(t)/cos(t))

Hence

1/2 sin(t)cos(t) < 1/2 t <  1/2sin(t)/cos(t)

or

cos(t) < t/sin(t) < 1/cos(t)

As t -> 0 both cos(t) and 1/cos(t) approach 1.  By the squeeze theorem, t/sin(t) -> 1 Hence

sin(t)/t -> 1

We will leave it to be read that lim  t-> 0 (cos(t)- 1)/t = 0

IV.  Derivative of f(x) = sin(x)

Theorem:  If f(x) = sin(x) then f'(x) = cos(x)

Proof:  We compute lim h-> 0 [sin(x + h) - sin(x)]/h

= lim h->0 [sin(x)cos(h) + sin(h)cos(x) - sin(x)]h

= lim h -> 0 [(sin(x)cos(h) - sin(x))/h + (sin(h)cos(x)/h)]

= sin(x) lim h ->0 [(cos(h) - 1)/h] + cos(x) lim h->0 [sin(h)/h]

= cos(x)

V.  d/dx cos(x)

Theorem:  If f(x) = cos(x) then f'(x) = sin(x)

Proof:  f(x) = cos(x) = sin(pi/2 - x)

Hence f'(x) = -cos(pi/2 - x) = -sin(x)

VI.  The other trig functions

Example: d/dx tan(x) = d/dx (sin(x)/cos(x)) = [cos(x)cos(x) - sin(x)(-sin(x))/(cos(x))²]

= 1/ (cos(x))² = sec² (x)

Exercise:  Show that

A.  d/dx cot(x) = -csc² (x)

B.  d/dx sec(x) = sec(x) tan(x)

C.  d/dx csc(x) = -csc(x)cot(x)

D.  d/dx ln(sec(x) + tan(x)) = sec(x)

E.  d/dx ln(sec(x) ) = tan(x)