Asymptotes

I.  Quiz

II.  Homework

III.  Definition of a Limit at Infinity

Let L be a real number and f(x) be a function.  Then

if for every e  > 0, there is an M > 0 such that  |f(x) - L| < e whenever x > M.

In other words as x gets very large f(x) gets very close to L.

If

then we say that f(x) has y = L as  a horizontal asymptote.

Example

Find the horizontal asymptote of

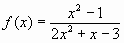
Solution:

Divide by x² on the numerator and the denominator to get

lim (1 - 1/x²)/(2 + 1/x - 3/x²) = lim (1/2) = 1/2.

We will attempt many more such limits.