I.  Quiz

II.  Homework

III.  Limits Using Tables

Consider the function f(x) =

Notice that this function is undefined at x = -1. In calculus undefined is not as precise as possible.  Instead one asks, what does the y value "look like" when the x value is near -1.  The table below demonstrates:

x	-0.9	-1.1	-0.99	-1.01	-0.999	-1.001
y	-1.9	-2.1	-1.99	-2.01	-1.999	-2.001

We see that if x is close to -1, then f(x) is close to -2.  We say "the limit of f(x) as x approaches -1 is -2" and write

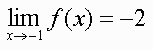
If the y value does not tend toward a single number as x tends towards a, then we say that the limit does not exist as x approaches a.  

Exercises:  Use a table to find the following limits if they exist.

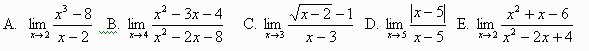
IV.  Limits and Graphs

Looking at the graph of a function is another convenient way of determining a limit.  For example, a computer was used to graph the the function

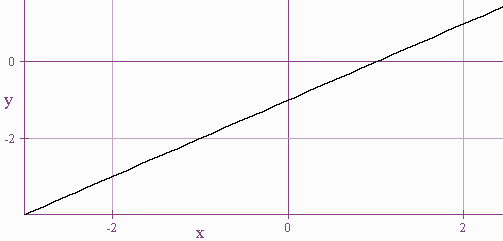
Notice that the computer indicates that the y value approaches -2 as the x value approaches -1.  In fact, the computer ignores the fact that the function is undefined at x = -1.  

Exercise:  Use a graphing calculator to find the limits from the prior exercise if they exist.  

V.  The Epsilon-Delta Game

Choose a function and a number.  Let partner A select a y range.  Partner B must find an x range so that the graph leaves the box on the sides and not the top and bottom.  If Partner B can always win, then the function has a limit at that number.  We will play this game first with me as Partner B and the class as Partner A.  Then the class will pair up and do it themselves.