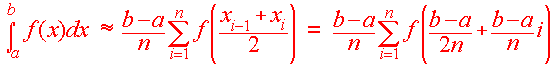Numerical Integration
Review of Left and Right Sums
We first encourage you to review left and right sums in class. For more information
click here
The Midpoint Approximation
To get a better approximation of , for example,
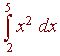
we could instead use the y-value of the midpoint of each
interval as the height. We will use six rectangles.
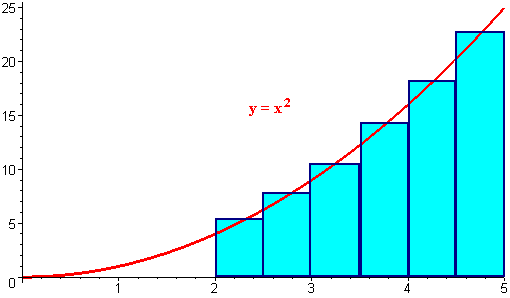
Notice that the first midpoint is at 2.25 and each rectangle width
5 - 2
Dx
=
= .5
6
The new numbers are as follows:
2.25 + 0(.5),
2.25 + 1(.5), 2.25 + 2(.5), 2.25 + 3(.5), 2.25 + 4(.5), 2.25 + 5(.5)
so that the y coordinates are
(2.25 + 0(.5))2, (2.25 + 1(.5))2, (2.25 + 2(.5))2, (2.25 + 3(.5))2, (2.25 + 4(.5))2, (2.25 + 5(.5))2
We see that the ith rectangle has y-coordinate:
height = (2.25 + i(.5))2
To get the area of the ith rectangle we multiply the height by the base:
(2.25 + i(.5))2(.5)
Finally to get the total area we add the terms up:
S(2.25 +
i(.5))2(.5) = 38.9975
The true solution is 37.66... . The left
endpoint approximation would have yielded 33.875
and the right endpoint approximation would have yielded 44.375.
We see that for this case, the midpoint approximation yields a closer
approximation.
This approximation is called the midpoint approximation
and is given in general by
|
|
The Trapezoidal Approximation
A fourth method involves the trapezoidal rule which geometrically calculates the area of the trapezoid with base on the x-axis and heights f(xi) and f(xi+1)
The area of the trapezoid is
Dx
( f(xi) + f(xi+1) )
2
or the base times the average of the heights. Adding
up all the trapeziods gives
|
b - a |
Example
Use the trapezoidal approximation with three trapezoids to approximate the integral
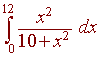
Solution
The picture is shown below.
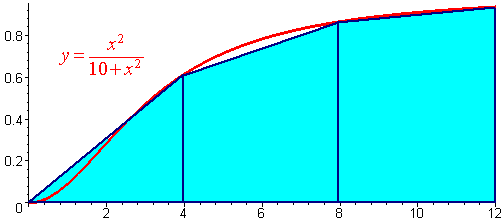
The x values of interest are
x0 = 0, x1 = 4, x2 = 8, x3 = 12
Plugging in these values into the function gives
f(0) = 0, f(4) = 0.6154, f(8) = 0.8649, f(12) = 0.9351
The trapezoid approximation formula gives
12 - 0
T(n) =
[0 + 2(0.6154) + 2(0.8649) + 0.9351]
2(3)
= 7.7914
We can compare this with the true answer of 7.8475.
Exercise
Use the Trapezoidal Approximation with 5 trap to approximate the integral
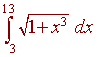
Error
The error in approximating an integral can be found by subtracting the true value from the estimated value. The graphs show that the error is directly inked to the concavity of the integrand. Without proof, bounds for the errors using the midpoint and trapezoid approximations are:
B(b - a)3
|EM| <
24n2
B(b - a)3
|ET| <
12n2
Where
B = max |f
''(x)|
Example:
If you want to approximate
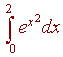
using the midpoint rule with an error of less than .001,
we compute
![]()
which in an increasing
function on [0,2], hence has its maximum at x =
2. So
B = (2 +
4(4))e4 < 983
so we find
983(23)
< .001
24n2
or
7864 < .001(24n2)
n2 < 327667
Taking square roots of both sides gives
n > 572
Hence if we let
n = 573
we are guaranteed to have an error less than .001.
Simpson's Estimate
We saw that the Trapezoidal and Midpoint estimates
provided better accuracy than the Left and Right endpoint estimates. It
turns out that a certain combination of the Trapezoid and Midpoint estimates is
even better.
|
Let f(x) be a function defined on
[a,b].
Then where T(n) and M(n) are the Trapezoidal and Midpoint Estimates. S(n) is called Simpson's Estimate for the integral |
Geometrically, if n is an even number then Simpson's Estimate
gives the area under the parabolas defined by connecting three adjacent points.
Let n be even then using the even subscripted x values for the
trapezoidal estimate and the midpoint estimate, gives
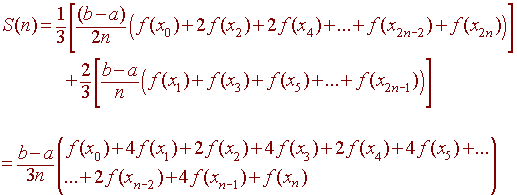
Notice the
1 2 4 2 4 ... 2 4 2 4 1
pattern.
Example
Use Simpson's Approximation with n = 6 to
approximate
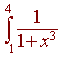
Solution
The key values of x are
x0 = 1, x1 = 1.5, x2 = 2, x3 = 2.5, x4 = 3, x5 = 3.5, x6 = 4
and the function values are
f(x0) = .5, f(x1) = .2286, f(x2) = .1111,
f(x3) = .0602, f(x4) = .0357, f(x5) = .0228, f(x6) = .0154
Now we can put these numbers into the Simpson's approximation formula.
4 - 1
(.5 + 4(.2286) + 2(.1111) + 4(.0602) + 2(.0357) + 4(.0228) + .0154)
3(6)
= .3426
Exercise
Use Simpson's approximation with n = 4 to approximate
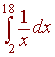
Without proof, we state
Let
M = max |f''''(x)|
and let ES be the error
in using Simpson's estimate then
M(b - a)5
|ES| <
180n4
Example
Determine the value of n that will approximate
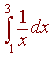
within two decimal places of accuracy.
Solution
We need to have an error less than .005:
|ES|
< .005
We have
b - a
= 3 - 1 = 2
We take derivatives to compute M:
f(x) = 1/x
f '(x) = -1/x2
f ''(x) = 2/x3
f '''(x) = -6/x4
f ''''(x) = 24/x5
We see that the maximum value of this function between 1 and
3 occurs when
x = 1:
M = |24/15|
= 24
We put this together to get
(24)(25)
< .005
180n4
Multiplying by the denominator gives
768 < 0.9 n4
or
853.33 < n4
Taking
fourth roots gives
n > 5.4
Hence, if we choose n = 6 we are guaranteed two decimals of accuracy.
Exercise
If you want to approximate
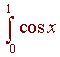
with n = 5, determine the maximum errors that occur using the midpoint, the trapezoidal, and Simpson's approximation.