How to Sketch the Derivative Graph Given the Graph of the Function

If we are given a graph and want to sketch the graph of the derivative, we just have to remember that the derivative is the slope of tangent line.  We can form a T-Table where the coordinates are (x, f '(x)). 

Example

Consider the graph shown below.  Sketch the graph of its derivative.

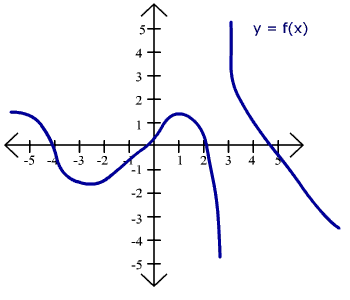
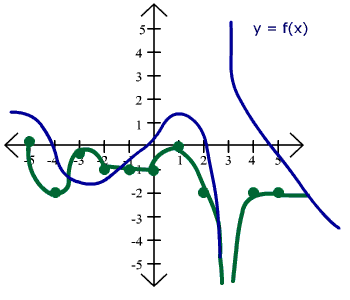
We will just eyeball the slope of the tangent line.  Notice that this slope is 0 for x = -2.5 and x = 1.  Now draw a T-Table of derivatives.  We start with x = -5.  The graph is almost horizontal but has a very slight downward slope.  Hence the derivative is approximately -0.2.  At x = -4, the graph is going downward but much steeper.  The slope of this tangent line is approximately -2.  At x = 3, the function is not continuous, hence it is undefined.  We write "DNE" to mean "Does Not Exist."

Now use the T-Table to plot the points.  (-5, -0.2), (-4, -2), etc.  Then connect the points with a curve.  The graph of the derivative is shown in green.