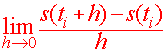Derivatives and Interpretations
Velocity
Recall that the difference between speed and velocity is that velocity has
direction and speed does not. In other words, the speed is the absolute
value of velocity. We have seen that the secant line can be used to
approximate the velocity. The formula for average velocity is
|
s(tf) - s(ti) |
If we want the instantaneous velocity we need to let tf equal ti. Unfortunately, this will always lead to and answer of 0/0 which is undefined. The solution is to take the limit as t2 approaches t1
We can think of t2 being just a little bit away from
t1, thinking of h as a small number, we can write
t2
= t1 + h
This leads us the following definition
|
Let s(t) be the position function, then the instantaneous velocity at ti is
|
Other words for the instantaneous velocity are:
velocity, derivative, slope, rate, marginal anything,...
Example:
The mars lander falls to the planet and has distance
function 10t2 with ground contact after 8
seconds. What
will be the exact impact velocity?
Solution 1:
We use the formula for instantaneous velocity
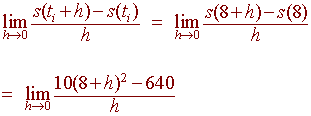
We cannot plug in 0 for h since we get 0/0, so we construct a table to approximate the limit:
| h | .01 | .001 | -.01 | -.001 |
| v | 160.1 | 160.01 | 159.9 | 159.99 |
We can guess that the instantaneous velocity is approximately 160,
but how can we tell that it isn't 159.9999999?
Solution 2:
We can graph the curve y = 10x2 and use the
zoom capabilities to approximate the slope of the tangent line at the point
(8, 640). Again the slope seems to be very close to 160.
Unfortunately, there is still no guarantee that this is exact. Click
here and
enter 10*x^2 for the function and 8
for x to try this.
Solution 3:
We calculate the limit:
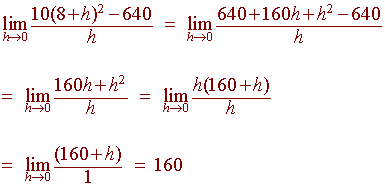
The third solution proves what we conjectured
after the first two approaches.
We have seen that the derivative gives the slope of the tangent line. We
can use this to find the equation of the tangent line at a point.
Example:
Find the equation of the tangent line to the curve
y = x2 +
x
at the point (1,2).
Solution:
To find the equation of a line we need a point and a slope.
The point is given as (1,2) and the slope can be calculated using the derivative:
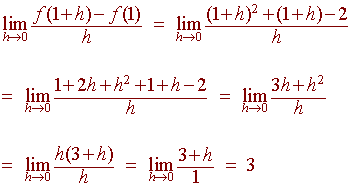
We can conclude that m = 3. The point-slope formula for a line gives
y - 2 = 3(x - 1)
or
y = 3x - 1
Exercise
Find the derivative of y = x-1/2
Other Derivative Sites
Derivative Problems and Solutions