The Chain Rule
The Chain Rule
Our goal is to differentiate functions such as
y = (3x + 1)10
The last thing that we would want to do is FOIL this out ten times.
We now look for a better way.
|
The Chain Rule
If
dy dy
du |
In our example we have
y = u10
and
u = 3x + 1
so that
dy dy
du
=
dx
du dx
= (10u9)(3) = 30(3x+1)9
Proof of the Chain Rule
Recall an alternate definition of the derivative:
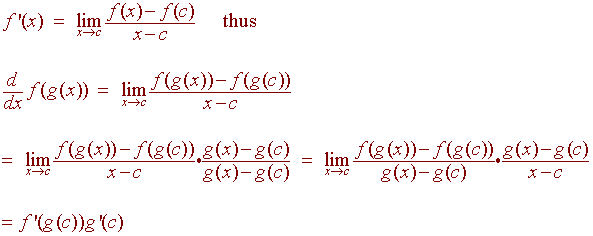
Example:
Find f '(x) if
-
f(x) = (x3 - x + 1)20
-
f(x) = (x4 - 3x3 + x)5
-
f(x) = (1 - x)9 (1-x2)4
-
(x3 + 4x - 3)7
f(x) =
(2x - 1)3
Solutions
Here
f(u) = u20
and
u(x) = x3 - x + 1
So that the derivative is
(20u19)(3x2 - 1) = [20(x3 - x + 1)19](3x2 - 1)
Here
f(u) = u5
and
u(x) = x4 - 3x3 + x
So that the derivative is
(5u4)(4x3 - 9x2 + 1) = [5(x4 - 3x3 + x)4](4x3 - 9x2 + 1)
Here we need both the product and the chain rule. First the product rule
f '(x) = [(1 - x)9][(1 - x2)4] ' + [(1 - x)9]' [(1 - x2)4]
Now compute
[(1 - x2)4]' = [4(1 - x2)3](-2x)
and
[(1 - x)9]' = [9(1 - x)8](-1)
Putting this all together gives
f '(x) = [(1 - x)9][4(1 - x2)3](-2x) - [9(1 - x)8] [(1 - x2)4]
Here we need both the quotient and the chain
rule.
(2x - 1)3[(x3 + 4x - 3)7]'
- (x3 + 4x - 3)7 [(2x - 1)3]'
f '(x) =
(2x - 1)6
We first compute
[(x3 + 4x - 3)7]'
= [7(x3 + 4x - 3)6](3x2 + 4)
and
[(2x - 1)3]'
= [3(2x - 1)2](2)
Putting this all together gives
7(2x - 1)3(x3
+ 4x - 3)6(3x2 + 4) + 6(x3 + 4x - 3)7
(2x - 1)2
f '(x) =
(2x - 1)6
Exercise
Find the derivative of
x2(5 - x3)4
f(x) =
3 - x
Other Derivative Sites
Chain Rule Problems and Solutions