Business Economics Applications
Review of Revenue, Cost and Profit
We define the revenue R to be the total amount of money coming into the company, the cost C the total amount of money coming out of the business, and the profit P is the revenue minus the cost. When we say marginal, we mean the derivative with respect to x the number of items sold.
For example the marginal cost is
dC
Marginal
Cost =
dx
If we let p be the price per unit, then we have
|
or R = px |
Example:
Suppose you own a snow board rental shop and have determined
that the demand equation for your snow boards is
x
p = $20 -
10
(At $20 per rental you wont sell any) and the cost equation is
C = 50 + 3x
($50 fixed costs and $3 per snow board rental) What is the marginal profit in terms of
x?
What price should you charge to maximize profits?
Solution:
The revenue is
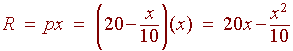
So that profit is
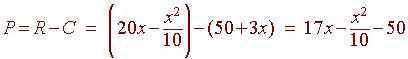
The marginal profit is
dP
x
= 17 -
dx
5
To find the maximum profit we set the marginal profit equal to zero and solve:
x
17 -
= 0
5
x = 105
Thus the price we should set is
105
p = 20 -
= $9.95 per rental
10
Exercise:
Suppose that the cost for a truck driver is $7.50 per hour and that the cost
to operate the truck is 0.002v2 where v is the average speed of
the truck. How fast should you recommend your driver to drive in order
to minimize the total costs?
Average
Recall that the average is the total divided by the number of items.
Hence, the average cost is the total cost
C divided by the average
cost x.
Example:
Find the minimum average cost if
C =
2x2 + 5x + 18
Solution:
The average cost is
C
18
A =
= 2x + 5 +
x
x
18
A' = 2 -
x2
We set
18
2 -
= 0
x2
to get
x = 3
Since
36
A'' =
x3
plugging in 3 gives a positive value. By the second
derivative test, we see that 3 is a minimum. The minimum average cost
is
Cmin
= 2(9) + 5(3) + 18 = 51
Exercise:
Find the maximum average revenue if the demand equation
is
p = 500 + 10x - x2
Elasticity
We define the price elasticity of demand by
|
Definition
rate of change of demand
We say that a product is elastic if |h| > 1 inelastic if |h| < 1
|
The idea is that a product is elastic if a drop in price results in a significant
rise in demand. A product is inelastic if a drop in price does not
result in a significant rise in demand.
Example
The demand function for a product is
p = 50 + x -
x2
determine the elasticity when x = 4.
Solution
We see that
p =
38,
dp/dx = 1 - 2x = -7
hence
38 /
4
38
h =
= -
-7
28
so that the product is elastic.
Exercise
Determine the elasticity for
x2
p =
at x = 10
100x - 1