Induction
-
Evaluating a Series
If we have a finite series there are two ways of evaluating it. The first way is computation by hand.Example:
Sn = 15 (2n-1)
is
1 + 3 + 5 + 7 + 9 = 25.
Notice that we just plugged in the values 1,2,3,4, and 5 for n and added up the results.Example:
Sn=2100 (1/n)
You can try this by hand, but you will become very bored and discouraged as you find out that you need to add up 100 numbers. Instead we use our calculator:
sum seq(1/x,x,2,100,1) = 4.187
we find the sum and seq features under Math -> Misc. sum means that we are adding up the terms, seq means that it is a sequence, 1/x is our function, x is our variable, 2 is where we start, 100 is where we stop, and 1 means that we are not skipping numbers.
-
Mathematical Induction
Suppose that we want to find
Si = 1100(i)
We can pair the first and last terms to get
1 + 100 = 101
then pair the second and penultimate term to get
2 + 99 + 101
again. We can do this repeatedly until we arrive at the 50th and 51st terms to get 101. in all we have
101(100)/2We can conjecture that for any n,
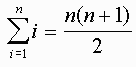
To prove this we use mathematical induction which means the following:
If the theorem is true for the first one and if the theorem is true for the next one given the truth of the preceding one, then the theorem is true for all n.
The steps for using induction are as follows:
-
Plug in n = 1 and verify the theorem.
-
We write: Assume that the theorem is true for n = k -1. Plug in k - 1 for n and write down the statement.
-
Write down the statement of the theorem for n = k by plugging in k for n.
-
Do some algebra or logic to write what you have in 3) as a part with the statement from 2 and other stuff.
-
Use the theorem for n = k - 1 to rewrite your expression from part 4.
-
Do more algebra to write the conclusion of the theorem for n = k
-
Write: "By induction we can conclude that the theorem is true."
For our example, we follow our steps:
-
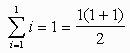 which checks.
which checks.
-
Assume that the theorem is true for n = k -1. Then
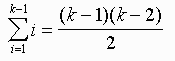
-
We write S i = 1k ( i)
-
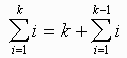
-
= k + (k - 1)(k)/2
-
= 2k/2 (k2 - k)/2 = (k2 + k)/2 = k(k + 1)/2
-
"By induction we can conclude that the theorem is true."
Exercise: Show that
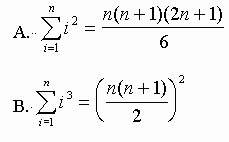
-
-
Second Principle of Mathematical Induction
To prove a theorem using induction, it is ok to assume that the theorem is true for all
n < kExercise
Let u = 1 1 1 0 and let un be the nth Fibonacci number, prove that
un = un+1 un un un-1 for all n > 2 -
For n = 2, we have
u2 = 2 1 1 1 which checks
-
Now assume that the theorem is true for n = k - 1, then
uk - 1 = un un-1 un-1 un-2
-
We have uk
-
= uuk - 1
-
= 1 1 1 0 un un-1 un-1 un-2 = un + un-1 un un-1 + un-2 un-1 -
= un+1 un un un-1 -
"By induction we can conclude that the theorem is true."
Bonus Exercise: The birthday paradox?
What is wrong with this use of induction?
Theorem?: For any group of people in a room they will all have the same birthday.
Proof by induction?: Assume that for any k - 1 people in a room that they all have the same birthday. For n = 1 the theorem is obviously true. Now suppose that are k people in a room. Send one person out. Now there are k - 1 people left in the room, so by the induction hypothesis they all have the same birthday. Send the person back in and send a different person out. Again there are k - 1 people in the room, so they all have the same birthday. Since the first person that was sent out has the same birthday as the rest of the group and so does the second person, everyone has the same person. Hence by induction, the theorem is true.
-
Back to the College Algebra Part II (Math 103B) Site
Back to the LTCC Math Department Page
e-mail Questions and Suggestions