Infinite Geometric Series

I.  Homework

II.  Definition of an Infinite Geometric Series

We learned that a geometric series has the form

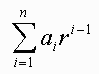
We call the series

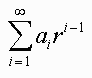
the infinite geometric series.  

III.  Calculating the Infinite Geometric Series

I will do the classic example of walking half way to the wall then walking half way and so on.  This demonstrates that

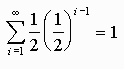
We say that this series converges to 1.

Suppose that r = 2 and a₁ = 1

then the infinite geometric series is

2 + 4 + 8 + 16 + ...

We see that these numbers just keep increasing to infinity.  

In general, if |r| > 1 then the geometric series is never defined.  We say that the series diverges.

If |r| < 1 then recall that the finite geometric series has the formula

sum from i = 1 to n of a₁r^i-1 = a₁[(1 - rⁿ)/(1 - r)]

If n is large then rⁿ will converge asymptotically to 0 and hence we have the formula

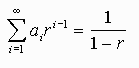
Example:  

Find sum from i = 1 to n of 2(1/3)^i-1

Solution:

We have 2/(1 - 1/3) = 2/(2/3) = 3

IV.  Repeating Decimals

Recall that a rational number in decimal form is defined as a number such that the digits repeat.  We can use a geometric series to find the fraction that corresponds to a repeating decimal.

Example:

.737373737... = .73 + .0073 + .000073 + ...

we have a₁ = .73 and r = .01 Hence

.73737373.... = .73/(1 - .01) = (73/100)/(99/100) = 73/99

V.  Interval Of Convergence 

If an infinite series involves a variable x, then we call the interval of convergence the set of all x such that the interval converges for that x.  For example

sum from i = 1 to infinity of x^i-1 has interval of convergence -1<x<1.

Example:  find the interval of convergence of

sum from i = 1 to infinity of (3x - 2)^i-1

We write |3x - 2| < 1 we solve

3x - 2 =1 or 3x - 2 = -1

x = 1 or x = 1/3

Hence 1/3 < x < 1 is the interval of convergence.