Exponentials

I.  Introductions and Hand Out Syllabus

II.  Example of an Exponential Function

A biologist grows bacteria in a culture.  If initially there were three grams of bacteria, after one day there are  six grams of bacteria, and after two days, there are twelve grams, how many grams will there be at the end of the week?

Solution:

We draw a t chart

t	P(t)
0	3 = 3(20)
1	6 = 3(21)
2	12 = 3(22)

We see that the general formula is

P(t) = 3(2^t)

Hence after one week, we calculate

P(7) = 3(2⁷) = 384 grams of bacteria.

We call P(t) and exponential function with base 2.

II.  Graphing Exponentials

We will graph this function on the TI 85.  

Then we will see that for any b > 1 the graph of y = b^t looks similar.

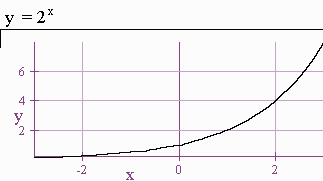
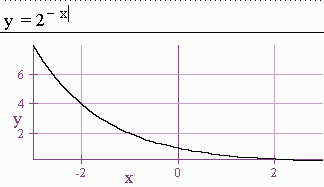
 Notice the left horizontal asymptote at 0.  We will then use shifting techniques to graph

y = 2^-x, y = -2^x, and -2^-x

III.  Three Properties of Exponents  

Property 1:  b^xb^y = b^x+y

Property 2:  b^x/b^y = b^x-y

Property 3:  (b^x)^y = b^xy

Definition:  b^-x  = 1/b^x

Exercise:  Simplify  3⁴(-3)^-1/[(3²)³]

IV.  Applications

Money and Compound Interest

We have the formula for compound interest

A = P(1 + r/n)^nt

where A corresponds to the amount in the account after t years in a bank that give an annual interest rate r compounded n times per year.

Suppose we have $2,000 to put into a savings account at a 4% interest rate compounded monthly.  How much will be in the account after 2 years?

We have P = 2,000, r = .04, n = 12 and t = 2.  We want A.

A = 2000(1 + .04/12)¹²⁽²⁾  = $2,166.29.

Continuous Interest

We have the formula:  A = Pe^rt

Inflation example:

With an 8% rate of inflation in the health industry, how much will health insurance cost in 45 years if currently I pay $200 per month?

Solution

We have r = .08, P = 200, and t = 45.  So that

A = 200e^(.08)(45) = $7319 per month! 

Note:  If you write "I love those math group projects" on your first homework assignment, then you will receive one extra point for that assignment.