Linear Programming
-
Linear Programming (An Example)
Example
Maximize
P = 2x + 5
subject to the constraints
x + 3y < 15
4x + y < 16
x > 0
y > 0
First we graph the system of inequalities.
-
For
x + 3y = 15
we use (0,5) and (15,0) and note that the arrows point towards (0,0).
-
For
4x + y = 16
we use (0,16) and (4,0) and note that the arrows point towards (0,0). -
x > 0 and y > 0 constrain the region in the first quadrant.
We have a closed and bounded region. (closed means that all the boundary lines are solid). We now need to find the largest value that
P = 2x + 5y
gives when (x,y) is inside the region. Lets try some guesses.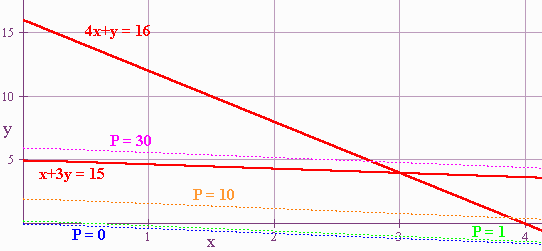
-
If P = 0 we can graph
2x + 5y = 0
and note that the graph is a line that intersects the region.
-
If P = 1 we can graph
2x + 5y = 1
and note that the graph is a straight line that intersects the region. Notice also that these lines are parallel.
-
If P = 10, we again get a parallel line that intersects the region.
-
If P = 30, we get a parallel line that does not intersect the region. Therefore, P must be smaller than 30.
We are searching for the parallel line that is farthest from the origin that intersects the region. this occurs at the corner point (3,4).
-
-
The Big Theorem
Fundamental Theorem of Linear Programming
If a linear programming problem has a solution, then the solution always occurs at a corner point. If two adjacent corner points give solutions, then every point on the line segment connecting them also give that solution. If the profit function isP = ax + by
then-
If the region is bounded , then P obtains both a maximum and a minimum.
-
If a and b are positive, then P will always have a minimum in the region if the region lies entirely within the first quadrant.
-
-
Step by Step Process
-
Graph the region and list the corner points in a table. You find the corner points by using matrices. Note if the region is bounded, or if we are looking for a minimum and that region is restricted to the first quadrant.
-
In the second column evaluate the Profit function
. -
If we are looking for a maximum, circle the largest number in the profit column. If there is a unique maximum then this is the solution. If there are two maxima, then the entire line segment between the two points gives a solution. If we are looking for a minimum, then circle the smallest number in the profit column, and proceed as before.
Example:
Maximize
80x + 50y
subject to the constraints
2x + y < 80
x + y < 50
x > 0
y > 0
We graph the equations and notice that there are three easy to find corner points:
(0,0), (40,0), (0,50)
The forth corner point is at the intersection of the two lines. The matrix is
A = 2 1 1 1
Note that the determinant is
2 - 1 = 1
so that a solution exists. We use a calculator to find
A-1 = 1 -1 -1 2 Hence the solution is
(30,20)
Now construct a profit table:
Point 80x + 50y (0,0) 0 (40,0) 3,200 (0,50) 2,500 (30,20) 3,400 Since the largest number is 3,400, we can conclude that the maximum occurs at the point (30,20) with a value of 3,400.
-
-
Linear Programming Applications
-
Solomon manufactures parabolic skis and conventional skis. The manufacturing process is done first at the fabricating department and then at the finishing department. The fabricating department has at most 108 labor hours per day available while the finishing department has at most 24 labor hours available per day. The parabolic ski requires 6 labor hours at the fabricating department and one labor hour at the finishing department. The conventional ski requires 4 labor hours at the fabricating department and one labor hour at the finishing department. Solomon makes a $40 profit on its parabolic skis and $30 on its conventional skis. How many of each type of ski should be manufactured each day to realize a maximum profit.
-
Harveys is planning to add an additional room to its casino. The casino consists of card tables and slot machines. On an average day, a slot machine makes $2,000, while a card table makes $30,000. The total square feet available at Harveys' new casino room for gaming is 3,000 square feet and the total number of additional employees allowed by the gaming commission is 45. If a slot machine occupies 6 square feet and requires one employee per 12 machines and a card table occupies 54 square feet and requires three employees per two tables, how many slot machines and how many card tables should be put into the new casino room in order to maximize profit? What is the maximum Profit? (Smaller tables are permitted)
-
A veterinarian wishes to prepare a supply of dog food by mixing Purina Big chunks and Alpo Meaties. The mixture is to contain at least 50 units of carbohydrates, at least 36 units of protein, and at least 40 units of fat. The Big Chunks contain 3 units of carbohydrates per pound, 3 units of protein per pound, and 2 units of fat per pound. The Meaties contain 5 units of carbohydrates per pound, 4 units of protein per pound, and 8 units of fat per pound. The veterinarian can purchase the Big Chunks for 44 cents per pound and the Meaties for 80 cents per pound. How many pounds of each dog food should be mixed in order to meet the dietary requirements at the least cost?
-
Back to the College Algebra Part II (Math 103B) Site
Back to the LTCC Math Department Page
e-mail Questions and Suggestions