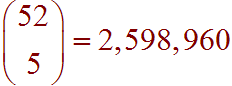Practice Final

Problem 1

Let

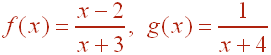
A.  Find the domain of  f o g(x).

Solution

Recall that x is not in the domain of the composite function if it is either not in the domain of the inner function or the inner function evaluated at x is not in the domain of the outer function.  The inner function g(x) is a rational function, hence the only values of x that are not in the domain will be zeros of the denominator.  That is x = -4.  Similarly the only value that is not in the domain of f(x) is -3.  We set

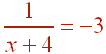
and solve.  We get

-3x - 12  =  1

or

x  =  -13/3

We can conclude that the domain is

{x | x ≠ -4, x ≠ -13/3}

B.  Find  f o g(x).

Solution

We find the composite function and simplify

Next simplify by multiply the four terms in the numerator and denominator by x + 4.

Problem 2

Let

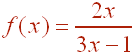
A.  Prove that f is a 1-1 function.

Solution

To prove that a function is 1-1, we must show that if f(a) = f(b) then a = b.  We have that if

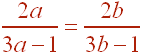
Now cross multiply to get

6ab - 2a  =  6ab - 2b

Next subtract 6ab from both sides to get

-2a  =  -2b

Finally divide both sides by -2 to get

a  =  b

Therefore f(x) is a 1-1 function

B.  Find the inverse of f.

Solution

To find the inverse of a function, we just switch the two variables and solve.

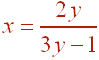
Multiply both sides by 3y - 1 to clear the denominator to get

3xy - x  =  2y

Next bring the y terms to the left hand side of the equation and the x to the right hand side to get

3xy - 2y  =  x

Factor out the y to get

(3x - 2) y  =  x

Finally divide by 3x - 2 on both sides to get

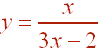
So that the inverse function is

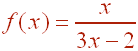
Problem 3

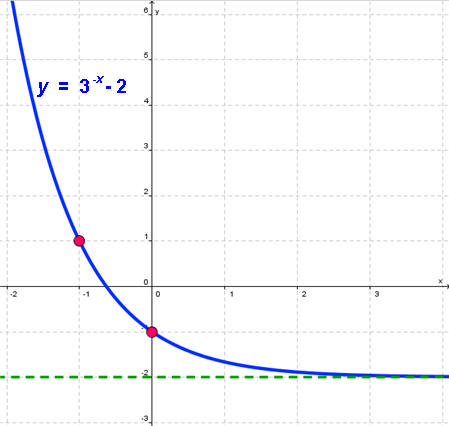
Sketch the graph of

This is the graph of the y = 3^x function reflected across the y-axis and shifted down 2.  The graph is shown below.

Problem 4

Put into exponential form to find the exact value of

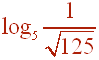
First we put this into exponential form.  If

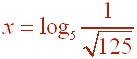
Then

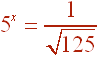
Next notice that 125 is the cube of 5 so that

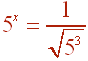
The square root is the same as the 1/2 power, so that

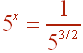
Finally, having a power in the denominator is the same as having a negative power in the numerator, so that

We can now equation exponents to get the solution.

x  =  -3/2

Problem 5

Write the expression as a sum and/or difference of logarithms.  Express powers as factors and simplify.

First we can use the rules of exponents that says that the log of a product of the sum of the log and the log of the quotient is the difference of the logs.  That is if the factor is in the numerator is will have a positive coefficient and if the factor is in the numerator then it will have a negative coefficient.  We get

Next, it is easier to write the square root as an exponent.

For the first two terms we can use the rule of logs that says that the log of a power is equal to the exponent time the log of the base. For the third term, we can cancel the ln and the e since they are inverse functions.

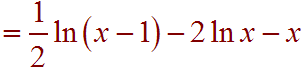
Problem 6

Solve the following equations. 

A. 

Solution

First use the log rule that says that a number times a log of something is the log of that something to the number.  That is, we can bring up the 2 as an exponent in the first term.

Now use the log rule that tells us that a difference of logs is the log of the quotient.

Next change to exponential form

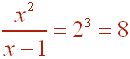
Multiply both sides by x - 1 to get

x²  =  8x - 8

Set this equation equal to 0 to get

x² - 8x + 8  =  0

We can now finish this up with the quadratic formula to get

B.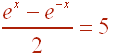 

Solution

First multiply both sides by 2.

e^x - e^-x  =  10

Next realize that a negative exponent is the same as bringing the term to the denominator.  We get

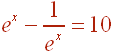
Multiply both sides by e^x to get

or

We can now use the quadratic formula to get

Now take ln of both sides to get

We can put this into a calculator to get

Problem 7

Brad, who is 21 years old, wants to invest $30,000 in a mutual fund that historically has grown 8% per year compounded continuously.   Brad figures he needs $1,000,000 to retire, at what age can Brad retire assuming that the mutual fund grows as it has historically throughout the investment period?

Solution

We use the formula for continuous compound interest

A = Pe^rt

We have

A  =  1,000,000,   P  =  30,000,     r  =  0.08

We plug in

1000000  =  30000e^0.08t

Divide by 30000 to get about

33.33  =  e^0.08t

Take ln of both sides to get

ln(33.33)  =  0.08t

Divide by 0.08 and put it into a calculator to get the approximate answer

t  =  44

Since Brad is 21 years old, we add 21 and conclude that Brad will be about 65 years old when he is ready for retirement.

Problem 8

The expected logistics growth model for the quagga muscle if it finds its way into Lake Tahoe is

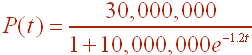
A.  Determine the carrying capacity for Lake Tahoe.

Solution

The carrying capacity is the population when t is very large, which makes the exponential go to 0, so that the denominator just becomes 1.  Thus the carrying capacity is just the numerator or 30,000,000.

B.  What is the growth rate of the muscle?

Solution

The growth rate is the coefficient in front of t, which is 1.2.

C.  Determine the initial population size.

Solution

The initial population is the population when t = 0, which is

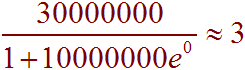
D.  Find the population 5 years after the muscle arrives.

Solution

We plug in 5 for t and use a calculator to get

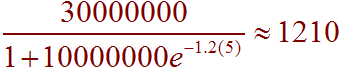
E.  When will the population be 20,000,000?

Solution

We set the P(t) equal to 20,000,000 and solve for t.

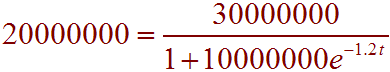
Multiply both sides by the denominator and then divide by 20,000,000 to get

1 + 10000000e^-1.2t = 1.5

Subtract 1 and divide by 10000000 to get

e^-1.2t  =  0.00000005

Now take ln of both sides to get

-1.2t  =  ln(0.00000005)

The calculator gives that the right hand side is about equal to -16.8.  Finally, divide both sides by -1.2 to get that

t  =  14

14 years after the quagga muscle is introduced there will be 20,000,000 quagga muscles in the lake.

Problem 9

Find the vertex, focus, and directrix of the parabola.  Then sketch the graph.

Solution

First put it in standard form by completing the square

x² + 6x + 9  =  9 + 7 - 4y

so that

(x + 3)²  =  -4y + 16

(x + 3)²  =  -4(y - 4)

We see that the vertex of the parabola is at the point (-3,4).  To find the focus, we set

-4  =  4a

so that

a  =  -1

Thus the focus is 1 below the vertex (below since the x term is squared and a is negative).  Thus the focus is at the point (-3,3).  The directrix is one above the vertex.  The directrix has coordinates (-3,5).  The graph is sketched below.

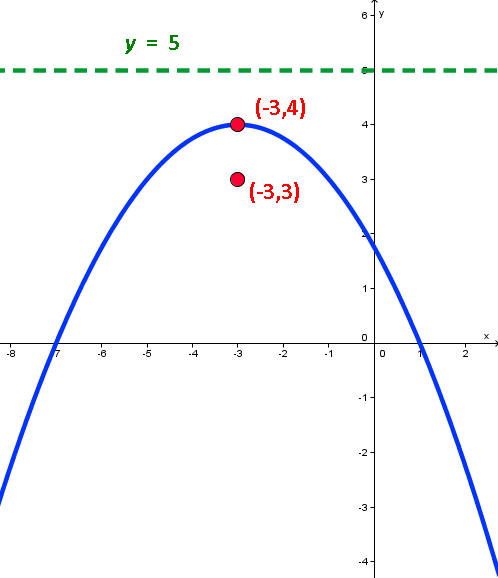
Problem 10

The aphelion of Jupiter is 507 million miles and the distance from the center of its elliptical orbit to the Sun is 23.2 million miles.  Find the perihelion and the mean distance.  Then write an equation for the orbit of Jupiter around the Sun.

Solution

It helps to sketch a diagram.  Recall that the aphelion is the farthest distance from the sun, the perihelion is the shortest distance, and the sun is at a focus.  The diagram is shown below.

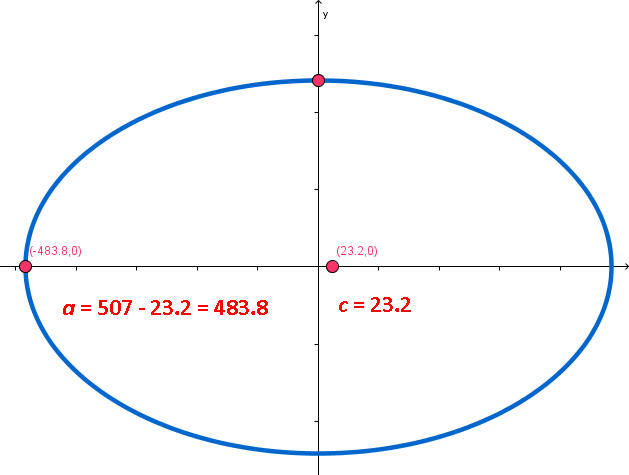
The mean distance is the distance from the center to the right side of the ellipse which is

483.8 million miles

The mean distance is the distance from the sun to the right hand side of the ellipse which is

483.8 - 23.2  =  460.6 million miles

To find the equation of the ellipse we need to find b which is the distance from the center to the top of the ellipse.  This is given by

Thus the equation of the elliptical orbit is given by

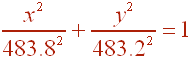
Problem 11

Find an equation for the hyperbola with center at (2,-1), focus at (2,4) and vertex at (2,2).  Then graph the equation.

Solution

The distance from the focus to the center is

4 - (-1)  =  5

so

c  =  5

The distance from the vertex to the center is

2 - (-1)  =  3

so

a  =  3

We use the formula to find a.

Therefore the equation of the hyperbola is

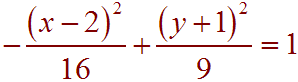
We sketch the fundamental rectangle that will help us sketch the graph of the hyperbola.  The graph is sketched below.

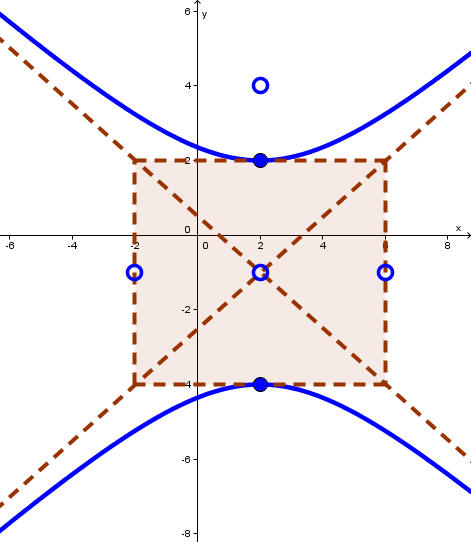
Problem 12

Solve the system of equations using an augmented matrix.  If the system has no solution say that it is inconsistent.

Solution

First we write down the augmented matrix by dropping the variables and turning the equal signs into a line.

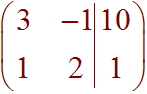
Next use row operations to put it in reduced row echelon form:

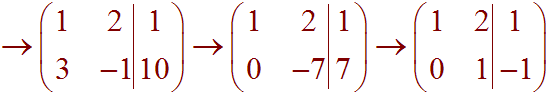
Now put this back into equation form.

x + 2y  =  1

      y  =  -1 

We can back substitute to find x. 

x + 2(-1)  =  1

x  =  3

Thus the solution is:  (3,-1).

Problem 13

Solve for x.

Solution

We take the determinant

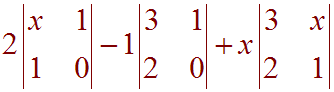
Now work each of these out to get

2[ (x)(0) - (1)(1) ] - 1[ (3)(0) - (1)(2) ] + x[ (3)(1) - (x)(2) ]  =  4x

This simplifies to

-2 + 2 + 3x - 2x²  =  4x

Which is

2x² + x  =  0

or

x(2x + 1)  =  0

So that

x  =  0     or     x = -1/2

Problem 14

Let

Find the each of the following that is defined.  If it is not defined, explain why.

AB, BA, A^-1, B^-1, A + 2B, 2A + A^-1

Solution

AB:

This is defined since A is a 2x2 matrix and B is a 2x3 matrix.  We get

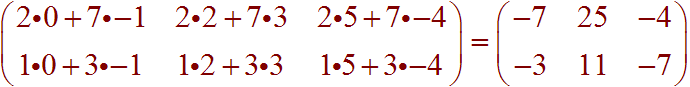
BA:

This is not defined since the number of rows of A is not equal to the number of columns of B.

A^-1:

This is defined since A is a square matrix.  We augment A with the identity and then use row operations to put the augmented matrix into reduced row echelon form.

Therefore the inverse matrix is

B^-1:

This is undefined, since B is not a square matrix.

A + 2B:

This is also undefined since we can only add matrices with the same dimension.

2A + A^-1:

This is defined since A and A^-1 are of the same dimension.  We have

Problem 15

Graph the system of inequalities.

Solution

First sketch the graphs as though they were equations instead of inequalities.  Notice that they are both parabolas; the first one is vertical opening upwards and the second one is sideways opening to the right .  To decide what to shade, use the test point of (0,0).  For the first inequality, we get

0  >  0² - 4

is a true statement, so the shading must go towards the origin for the first curve. 

For the second inequality we get

0  <  0² - 5

is false, so the shading must go away the origin. 

Finally shade in the regions where both inequalities are true.  The sketch is shown below.

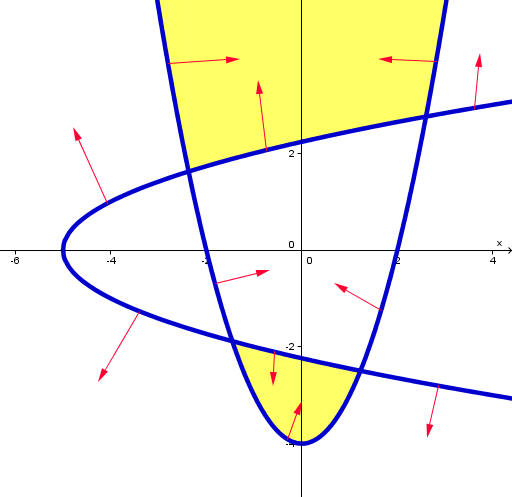
Problem 16

A casino needs to determine how many slot machines and how many table games to put in its 6000 square foot room so that it staff of 64 employees can manage the games.  Every ten machines takes one employee and 120 square feet of floor space, while each table requires two employees and takes us 100 square feet of floor space.  Each group of 10 slot machines brings in a profit of $4,000 and each table brings in a profit of $6,000.  How many slot machines and how many tables should the casino host in order to maximize profit?

Solution

This is a linear programming problem.  Let x equal the the number of groups of 10 slot machines and y equal the number of tables.  Since the room is 6000 square feet and the slot machine groups each use 120 square feet and the tables use 100 square feet, we get the inequality

120x + 100y  <  6000

Since there are 64 employees and each group of 10 slots machines requires 1 employee and each table requires 2 employees, we get

x + 2y  <  64

We also have that both variables must be nonnegative since it does not make sense to have a negative number of slot machines or a negative number of tables.  This gives us

x  >  0

y  >  0

Next sketch the shaded in region.  It is shown below.

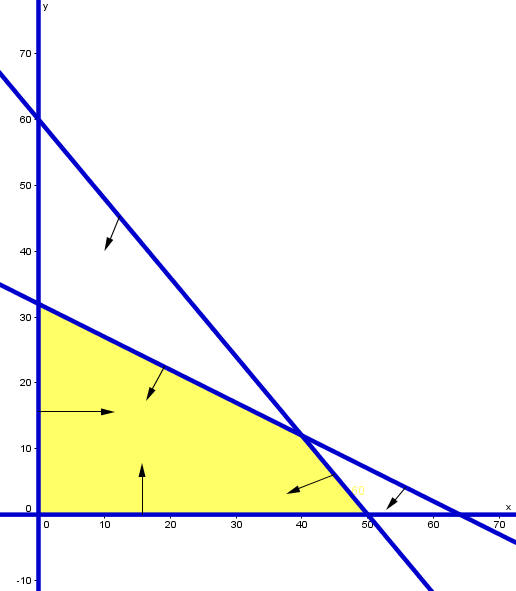
We see that the shaded in region is a quadrilateral with vertices (0,0), (50,0), (40,12), and (0,32).  The profit equation is

P(x,y)  =  4000x + 6000y

Next plug each of the four vertices into the profit equation.

We see that the maximum profit occurs at the point (40,12).  The casino should put in 400 slot machines (40 groups of 10) and 12 tables.

Problem 17

Write down the n^th term of the sequence suggested by the pattern

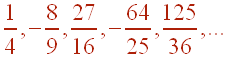
Solution

We can look at the three components of each term:  the numerator, the denominator, and the sign.  The numerator consists of perfect cubes.  Since the first number is 1 = 1³ no shifting is needed.  The denominator consists of perfect squares.  The first term is 4 = 2² thus we must add 1 to n before squaring.  The signs alternate from positive to negative and back.  Since the first term is positive, we need a (-1)^n-1.  Putting this all together gives

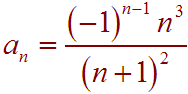
Problem 18

Given that

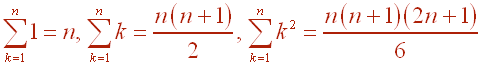
Find

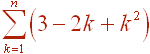
Solution

We can break it apart and distribute the constants:

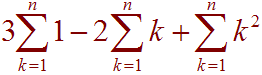
Now use the formulas to get

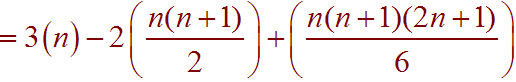
Problem 19

The 12^th term of an arithmetic sequence is 7 and the 18^th term is 31.  Find the 5th term.

Solution

Since the 12^th term is 7, we can use the formula for the general term of an arithmetic sequence to get

7  =  a₁ + d(12 - 1)

7  =  a₁ + 11d

Since the 18th term is 31, we get

31  =  a₁ + d(18 - 1)

31  =  a₁ + 17d

Subtracting the first equation from the second gives

24  =  6d

or

d  =  4

Plugging back into the first equation gives

7 = a₁ + 11(4)

so that

a₁  =  -37

To find the 5^th term, use the formula again

a₅  =  -37 + 4(5-1)  =  -21

Problem 20

The new city theater will have 18 seats in the first row and each successive row will contain two additional seats.  If there are 35 rows in the theater, how many seats will there be total?

Solution

It is helpful to list the first few terms:

18, 20, 22, 24

We see that this is an arithmetic sequence with first term 18 and common difference 2.  We want the sum of the first 35 terms.  In order to use the formula for an arithmetic series, we first need the last term, a₃₅.  We get

a₃₅  =  18 + 2(35 - 1)  =  86

Now we can use the arithmetic series formula.

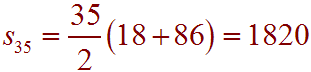
There will be 1820 seats in the new city theater.

Problem 21

Suppose that the second term of a geometric sequence is 2/27 and the fifth term is 6.  Find the sum of the first ten terms.

Solution

Since the second term of the geometric sequence is 2/9, we have

2/27  =  a₁ r^2-1  =  a₁ r

Since the fifth term is 6, we have

6  =  a₁ r^6-1  =  a₁ r⁵

Solving for a₁ in the first equation gives

a₁  =  (2/27)(1/r)

Plugging this into the second equation gives

6  =  (2/27)(1/r) r⁵  = 2/27 r⁴

Now solve for r.

81  =  r⁴

r  =  ±3

Thus

a₁  =  (2/27)(1/±3)  =  ±2/81

Now plug into the geometric sequence formula

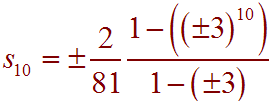
Putting this into a calculator gives the two possible answers:  -59048/81 and -29524/81.

Problem 22

The government is giving a $1,000 stimulus check to each citizen.  They figure that everyone will spend half of their money and 12% will come back to the government as taxes.  The vendors that collect the spent money will in turn spend half of their sales and 12 percent of the amount spent will go to taxes.  Then of this spent money, half will be spent again and 12% will come back as taxes.  If this continues forever, how much tax revenue will the government receive in total?

Solution

Notice that if half of the after tax money is spent.  Since the tax rate is 0.12, the after tax money is 0.88.  Half of this is 0.44.  We write down the first few terms of spent money. 

500, 500*0.44, 500*0.44², 500*0.44³, 500*0.44⁴

The total amount spent is a geometric series with first term 500 and common ratio 0.44.  We can use the formula of an infinite geometric series to get

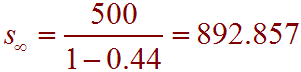
To find out the total tax revenue, take 12% of this number to get

Tax  =  (0.12)(892.857)  =  147.143

The government will reclaim about $147.14 from the initial stimulus check.

Problem 23

Use Mathematical Induction to prove that the statement is true for all natural numbers:

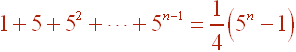
Solution

We first show that the statement is true for n = 1.  The left hand side of the equation is just 1, since with n - 1 = 0 and 5⁰ = 1.  The right hand side of the equation is

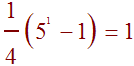
Therefore the statement is true for n = 1.  The nest step is to assume that the statement is true for n = k.  This means

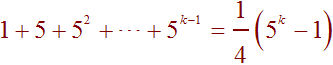
Now we need to use the above to show that the statement is true for n = k + 1.  We work on the left hand side.  It is helpful to not just include the first three and the last term in the sum but also include the second to last term.  The left hand side is

Notice that if we look at all but the last term, this is the left hand side of the induction hypothesis.  We can replace this with the right hand side of the induction hypothesis.

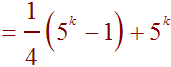
Now put everything over the common denominator 4.

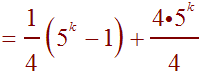
Simplifying gives

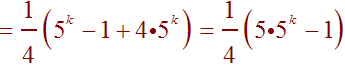
We can now use the rule of exponents to arrive at our goal.

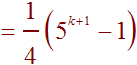
By mathematical induction the statement is true.

Problem 24

Prove that if a sequence is defined recursively by

Then the closed form of the sequence is

Solution

We use mathematical induction.  For n = 1, the right hand side of the statement becomes

ar^1-1  =  ar⁰  =  a

So the statement is true for n = 1.  Now assume that the statement is true for n = k.  Then

a_k  =  ar^k-1

We need to show that this implies that the statement is true for n = k + 1.  We have

a_k+1  =  ra_k+1-1  =  ra_k

Now we can use the induction hypothesis to get that this expression is equal to

=  r(ar^k-1)  =  ar^k

Thus by mathematical induction the statement is true.

Problem 25

Expand using the Binomial Theorem

Solution

We use the binomial theorem with the first term x² and the second term -2y. 

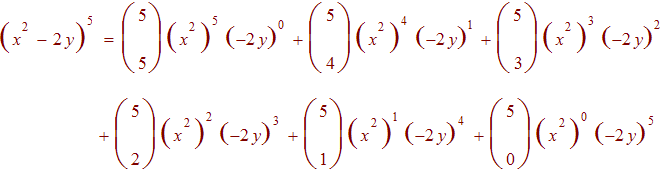
This is equal to

Finally, multiply the numbers together to get

Problem 26

Find the coefficient of x^3/2 in the expansion of

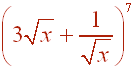
Solution

We use the binomial theorem noting that the k^th term is

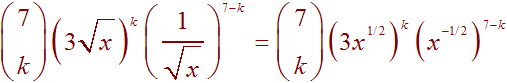
Next use the rule of exponents to get

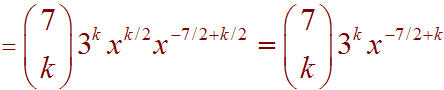
We want the x^3/2 term, so we set

-7/2 + k  =  3/2

so that

k  =  5

Finally just plug in to the coefficient to get

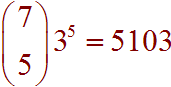
Problem 27

How many different 12-letter words (real or imaginary) can be formed from letters in the word "TAHOECOLLEGE"?

Solution

It helps to put the letters in alphabetical order.

ACEEEGHLLOOT

Notice that the repeats are:

3 E's,    2 L's,     2 O's

We can use the formula for counting the number of permutations of objects that are not distinct.  This number is

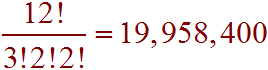
Problem 28

A poker hand consists of five cards from a 52 card deck.  The same five cards dealt in different orders count as the same poker hand.  How many different poker hands are there?

Solution

Since order does not matter, this is a combination problem.  We are choosing 5 objects from 52 objects.  The number of ways of doing this is