Practice Exam 2

Problem 1

Find the equation of the parabola with focus at the point (3,1) and directrix y = -5.  Then graph the parabola by hand.

Solution

It helps to sketch the graph first.  Notice that the vertex is always the midpoint of the focus and the directrix (the point on the directrix closest to the focus).  Thus the vertex is at the point (3,-2).

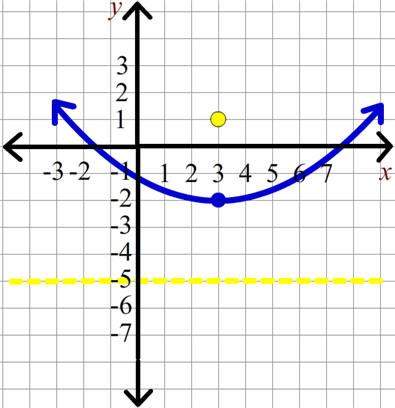
Parabola with focus (3,1), vertex (3,-2), and directix y=-5

We have that a is the distance from the vertex to the focus which is 3.  Since the directrix is horizontal, the parabola's equation has the form

(x - h)2  =  4a(y - k)

Plugging in gives

(x - 3)2  =  4(3)(y + 2)

or

(x - 3)2  =  12(y + 2)

 

Problem 2

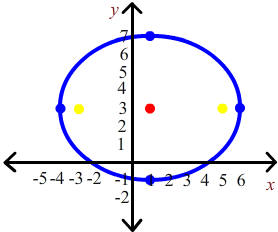
Find the equation of the ellipse with foci at (-3,3) and (5,3) and vertex at (-4,3).  Then graph the ellipse by hand.

Solution

First we find the center, which is always the midpoint between the tow foci.  For the x-coordinate, we find the average of -3 and 5 to be 1.  The y-coordinate is 3.  Thus the center has coordinates (1,3).  We have that c is the distance between the center and the focus which is 4.  a is the distance from the center to the vertex which is 5.  Next use the formula

b2  =  a2 - c2

Plugging in gives

b2  =  25 - 16  =  9

Therefore the equation of the ellipse is

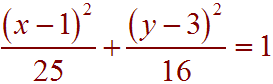
(x-1)^2 / 25 + (y-3)^2 / 16 = 1

The graph is shown below.

Ellipse with vertices (-4,3), (6,3), (1,-1), (1,7), center (1,3), and foci (-3,3) and (5,3)

 

 

Problem 3

Find the equation of the hyperbola with vertices at (-3,2) and (1,2) and asymptote y = 2x + 4.

Solution

The center of a hyperbola is always the midpoint between the two vertices.  The x-coordinate of the center is -1 and the y-coordinate is 2.  The coordinates of the center is (-1,2).

We have that a is the distance between the center and the vertex, thus a = 2.  The (positive) slope of the asymptote is b/a, so that

b/2  =  2

Thus b  =  4.

The equation of the hyperbola is

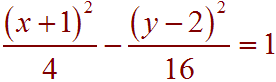
(x+1)^2 / 4 - (y-2)^2 / 16 = 1

The graph is shown below

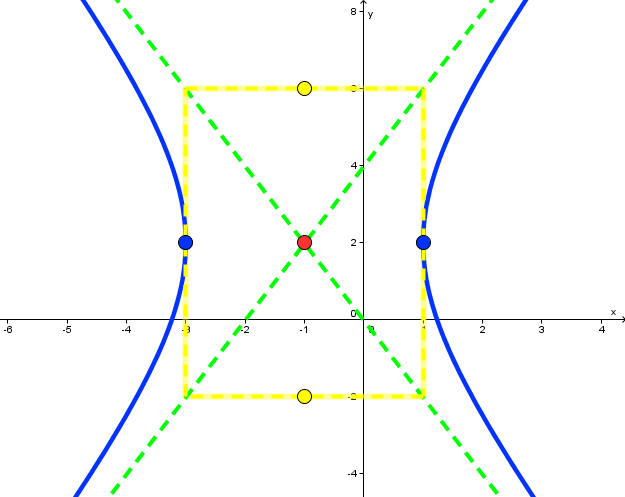
Hyperbola (x+1)^2 / 4 - (y-2)^2 / 16 = 1

 

 

Problem 4

Identify the type of conic each is.  Then find the any applicable feature: center, vertices, foci, directrix, asymptotes.

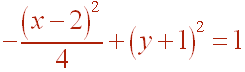
A.  -(x-2)^2/4 + (y+1)^2 = 1

Solution

Since both the x-terms and the y-terms are squared, it is not a parabola.  Since the x-term has a negative outside and the y-term does not, it is a hyperbola.  The center is at (2,-1).  We have a = 2 and b = 1.  Thus the vertices are at:  (2,-2) and (2,0).  The slopes of the asymptotes are 1/2 and -1/2.  To find the equation of the asymptotes, they both pass through the center (2,-1) so we use the point slope form to get

y - (-1)  =  1/2 (x - 2)

y  =  1/2 x - 2

and

y - (-1)  =  -1/2 (x - 2)

y  =  -1/2 x

For the foci, use the equation

c2 =  a2 + b2

c2 =  22 + 12 =  5

so that

c = root(5) 

The foci are at the points

(2,-1-root(5)) and (2,-1+root(5)) 

 

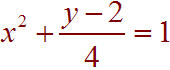
B.  x^2 + (y-2)/4 = 1

Solution

Since only one of the two terms is squared, this is a parabola.  We can multiply all three terms by 4 to get

4x2 + y - 2  =  4

or

y - 6  =  -4x2

The parabola has vertex (0,6).  We have that

1/4p  =  -4

so that

p = -1/16

so that the focus is at (0,95/16) and the directrix is the line y = 97/16.

 

C.  4x^2+y^2 -6y = 27

Solution

Since both x and y are squared, it is not a parabola.  Since the coefficients of these square terms are both positive and different it is an ellipse.  To find the center, we need to complete the square for the y-terms.  We find

(6/2)^2 = 9

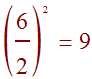
Thus we need to add 9 to both sides.

4x2 + y2 - 6y + 9  =  27 + 9

4x2 + (y - 3)2  =  36

Finally divide by 36 to get

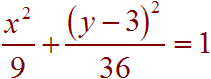
x^2 / 9 + (y-3)^2 / 36 = 1

The center of the ellipse is at (0,3).  We have a  = 6 and b = 3.  The vertices are at (0,-3) and (0,9).  To find the foci, we use

c2  =  a2 - b2

c2  =  36 - 9  =  27

c = 3root(3)

The foci are at the points

(0,3+3root(3)) and (0,3-3root(3))

 

Problem 5

Solve each system of equations using matrices.  If the system has no solution say that it is inconsistent.

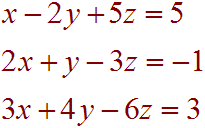
A.  x-2y+5z=5, 2x+y-3z=-1, 3x+4y-6z=3

Solution

First set up the associated augmented matrix.

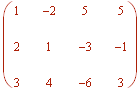
Matrix: 1 -2 5 5, 2 1 -3 -1, 3 4 -6 3

Next perform row operations to get it into row echelon form:

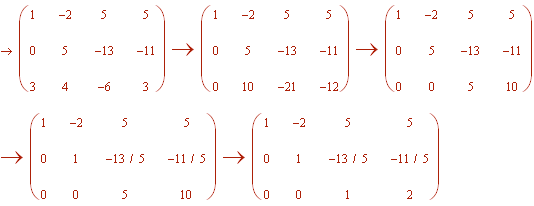
Row Operations that lead to the matrix: 1 -2 5 5, 0 1 -13/5 -11/5, 0 0 1 2

Next put it back into equation form

x- 2y + 5z  =  5

y  - 13/5 z =  -11/5

z  =  2

Now back substitute to get

y - 13/5 (2)  =  -11/5

y  =  3

 

x - 2(3) + 5(2)  =  5

x  =  1

The solution is (1,3,2).

 

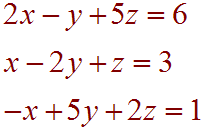
B.  2x-y+5z=6, x-2y+z=3, -x+5y+2z=1

Solution

First set up the associated augmented matrix.

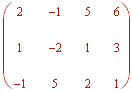
Matrix: 2 -1 5 6, 1 -2 1 3, -1 5 2 1

Next perform row operations to get it into row echelon form:

row ops produce row echelon form

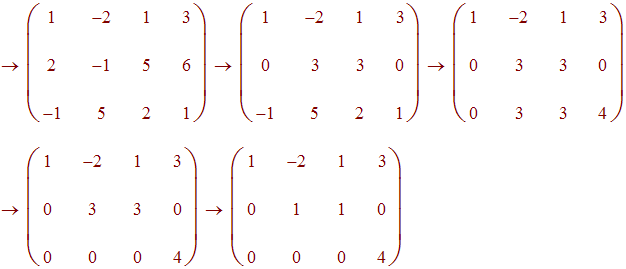
Next put it back into equation form

x - 2y + z  =  3

y + z  =  0

0  =  4

Since the last equality is a contradiction, there is no solution to this system of equations.

 

Problem 6 

Find the determinant of the following matrix (without using a calculator).

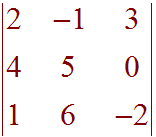
Matrix: 2 -1 3, 4 5 0, 1 6 -2

Solution

Expand by the first row:

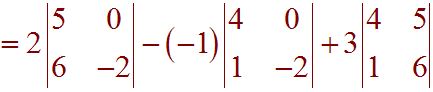
=2|5 0, 6 -2| - (-1)|4 0, 1 -2| + 3|4 5, 1 6|

Now just find the determinant of each of the 2x2 matrices:

2[(5)(-2) - (0)(6)] + [(4)(-2) - (0)(1)] + 3[(4)(6) - (5)(1)]

=  2[-10] + [-8] + 3[19]

=  -20 - 8 + 57

=  29

 

Problem 7

 Use Cramer's Rule (without using a calculator) if it is applicable to solve the system. 

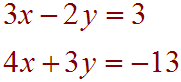
3x-2y = 3, 4x+3y = -13

Solution

Recall that Cramer's Rule gives the solution in terms of determinants.

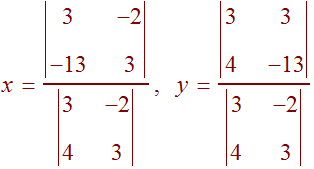
x = |3 -2, -13 3|/|3 -2, 4 3|, y = |3 3, 4 -13|/|3 -2, 4 3|

Now just compute the determinants to get

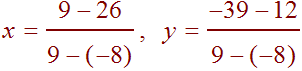
x=(9-26)/(9-(-8)), y = (-39-12)/(9-(-8))

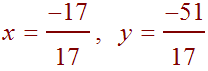
x = -17/17, y = -51/17

So that

x  =  -1,  y  =  -3

 

Problem 8

Given that

 Det[ a b c, 1 2 3, x y z ] = 5

Use the properties of determinants to find

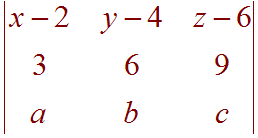
Det[ x-2 y-4 z-6, 3 6 9, a b c

Solution

Notice that the second matrix is obtained by taking the first matrix and first switching the first and third rows:

matrix: [ x y z, 1 2 3, a b c ]

Switching rows multiplies the determinant by -1, hence the determinant of this second matrix is -5.  Next replace the first row by the sum of the first row and (-2) times the second row to get:

matrix: [ x-2 y-4 z-6, 1 2 3, a b c ]

This row operation leaves the determinant unchanged.  So the determinant of this third matrix is still -5.  Finally multiply the second matrix by 3 to arrive at the goal matrix.   Multiplying a row by a constant multiplies the determinant by that same constant.  Thus the determinant of the goal matrix is

(3)(-5)  =  -15

 

Problem 9

A.  Find the inverse of the matrix

Matrix: [1 2 0, 0 2 2, 1 0 -1] 

Solution

We augment this matrix with the identity and then put it into reduced row echelon form.

Augment and use row ops to get: [1 0 0 -1 1 2, 0 1 0 1 -1/2 -1, 0 0 1 -1 1 1]

Therefore the inverse is the right hand side matrix:

Matrix: [-1 1 2, 1 -1/2 -1, -1 1 1]

 

B.  Use the result from part A. to solve the system:

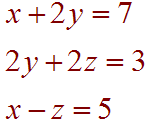
x+2y=7, 2y+2z=3, x-z=5

Solution

We can think of this system of equations as the matrix equation

Ax =  b

Where b is the right hand side of the equations.  This has solution

x  =  A-1b

or

[x, y, z] = [1 1 2, 1 -1/2 -1, -1 1 1] * [7, 3, 5] = [6, 1/2, 1]

 

Problem 10

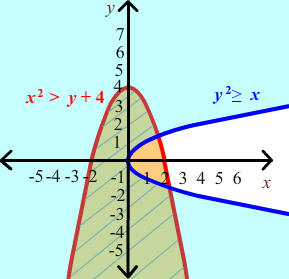
Graph the system of inequalities

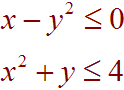
x-y^2 <=0, x^2+y <= 4 

Solution

First graph the two equations, noticing that they are both parabolas:

y2  >  x

y  <  4 - x2

Then notice that the first inequality will be false for large x, so the solution must lie to the left of the first graph.  The second graph is true for large y, so the solution lies above of the second graph.  We can also use test points.  We select a point in each of the regions cut out by the graphs.  We have

(0,5):  The second inequality is false since 5 < 4 - 02 is false.

(5,0):  The first inequality is false since 02 > 5 is false.

(1,0):  The first inequality is false since 02 > 1 is false.

(0,2):  Both inequalities are true.  Therefore this point is in the solution region which is the region with the slanted lines.

The solution is shown below.

solution to the system of inequalities

 

 

 

Problem 11

A science museum is constructing a whispering gallery that will be 150 feet in length.  The foci are located 50 feet from the center.  How high will  the ceiling be at the center?

Solution

A whispering gallery is in the shape of an ellipse (or at least a semi-ellipse).  It helps to sketch the picture

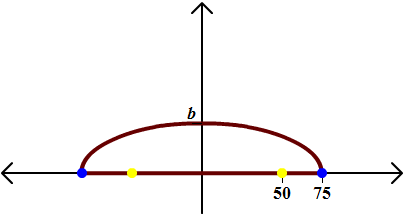
Ellipse with focus at (50,0) and vertex at (75,0)

We have

a  =  75,    c  =  50

Now just find b, which is the height of the gallery.  We have

b = root(a^2-c^2) = root(75^5-50^2) = 55.9

We can conclude that the ceiling is approximately 55.9 feet high.

 

Problem 12

Jordan and Yesha are each have loans from both Bank of America and Wells Fargo.  The first table shows the amounts borrowed and the second gives the interest rate per month. 

  B of A Wells Fargo
Jordan $8000 $4000
Yesha $6000 $5000
       
Monthly Interest Rates
B of A 0.008
Wells Fargo 0.01

A.  Write a matrix A for the amounts borrowed by each student and a matrix B for the monthly interest rates.

Solution

A and B are just the matrices that correspond to the first and second tables. 

A=Matrix[8000 4000,6000 5000], B=Matrix[0.008,0.01]

 

B.  Compute AB and interpret the results using a complete sentence.

We multiply

AB=Matrix[(8000)(0.008)+(4000)(0.01),(6000)(0.008)+(5000)(0.01)]=Matrix[104,98]

We can say that the total interested that Jordan will pay is $104 and the total interest that Yesha will pay is $0.01.

 

Problem 13

A nutritionist wants to make a cereal mix that contains at least seven grams of fiber and at least 200 grams of carbohydrates.  The first cereal of the mix will be raison bran that contains 5 grams of fiber per cup and 100 grams of carbohydrates per cup.  One cup of raison brand cost 30 cents.  The second cereal of the mix will be wheat chex that contains 3 grams of fiber and 110 grams of carbohydrates per cup.  One cup of wheat chex costs 25 cents.  How many cups of each type of cereal should be in the mix in order to minimize the cost of the cereal?

Solution

We label variables:

x  =  cups of raison bran

y  =  cups of wheat chex

The information gives the system of inequailities

5x + 3y  > 7

100x + 110y > 200

x > 0

y > 0

and the optimization equation

C  =  30x + 25y

The graph is shown below

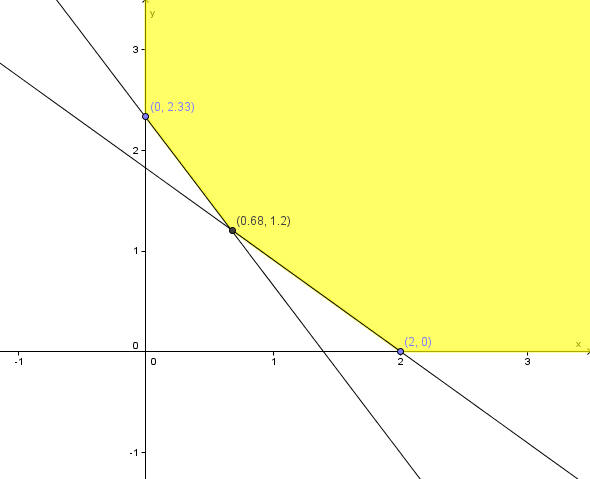
Shaded graph in Q1 above (2,0), (0,68,1.2), (0,2.35)

The minimum cost must occur at one of the vertices.  We compute the cost for each of the vertices to see which is the smallest:

30(2) + 25(0)  =  60

30(0.68) + 25(1.2)  =  50.4

30(0) + 25(2.33)  =  58.25

Since the second point corresponds with the lowest cost, the nutritionist should use 0.68 cups of raison bran and 1.2 cups of wheat chex.