The Parabola

Algebraic Definition of The Parabola

Recall that  the standard equation of the parabola is given by
        

y = a(x - h)2 + k

If we are given the equation of a parabola

        y = ax² +bx + c

we can complete the square to get the parabola in standard form.

Geometry of the Parabola

We can define a parabola as follows:

Geometric Definition of the Parabola Let F be a point on the plane and let y = -p be horizontal line called the directrix.  Then the set of points P such that FP is equal to the distance from the line to P is a parabola.

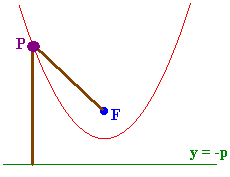
Example

Let 

        F = (0,2) 

and 

        y = -2 

be the directrix.  Then

        FP = (x² + (y - 2)²)^1/2 

and the distance from P to the directrix is given by

        2 + y

Hence

        2 + y =  (x² + (y - 2)²)^1/2 

squaring both sides, we get

        4 + 4y + y² = (x² + (y - 2)²) =  x² + y² - 4y + 4

We have 

        8y = x²  

or
        y = x²/8

In general if 

        y = -p 

is the equation of the directrix and 

        V = (h,k) 

is the vertex, then the Focus is at the point 

        F  =  (h,k + p) 

and the equation of the parabola is

y = 1/4p (x - h)2 + k

Note that vertex will always be half way between the focus and the directrix.

Example:

Find the equation of the parabola with Focus at (1,2)  and directrix y = -4.

Solution

We see that the vertex is at the point 

        (1, (-4+2)/2) = (1,-1)

Since the directrix is y = -4, we have

        p  =  4

so that

        1/4p  =  1/16

Hence the equation is

        y = -1/16 (x - 1)² - 1

Optics

Why the word focus?  

Application 1: 

A flashlight.
If a flashlight is to be 3 in in diameter and 2 inches deep, where should the bulb be placed?

Solution:

If the bulb is placed at the focus then the reflected light rays from the bulb will all travel in straight parallel lines outward.  We know that 

        y  = 1/4p x²

so that 

        2 = 1/4p (1.5)²

Solving gives

        8p = 2.25 or p = 0.28125 inches

Exercise:  Frying an Insect

Suppose that you have a magnifying glass that is 3 inches in diameter and .5 inched deep.  How high above the ground should you hold the magnifying glass so that it burns a hole in a leaf on the ground?

Back to the College Algebra Part II (Math 103B) Site

Back to the LTCC Math Department Page

e-mail Questions and Suggestions