Polynomials and Graphs

Polynomials and Graphs

Left and Right Behavior
We will investigate the outer shape of several polynomials and explore the following rules:

Even Odd

Pos UU DU

Neg DD UD

Where Even and Odd refers to the degree of the polynomial, Pos and Neg refers to the leading coefficient, And a U or a D refers to the left and right behavior of the curve.
Example
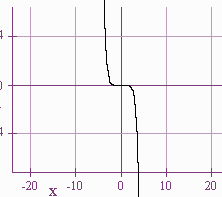
-3x⁷ + 4x⁴ - 1
has degree 7 which is odd and has leading coefficient -3 which is negative. Hence the left and right behavior is UD, i.e. the curve goes up on the left and down on the right.
Max and Min

Theorem
If f(x) is a polynomial of degree n then f(x) has at most n - 1 relative extrema. Where relative extrema are lumps of the graph.

Example:
4x⁵ + 2x³ - x² + 7x + 12
Has at most 4 relative extrema.
Three Step Procedure For Graphing Polynomials

Step 1: Factor the polynomial into linear factors of the form

ax + b
Step 2 : Determine the left and right behavior of the graph and the shape of the graph near each x intercept.
Step 3: Connect the dots.

Example:
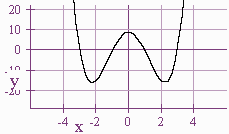
Graph

y = x⁴ - 10x² + 9
1. We have
  
  y = (x² -9)(x² - 1) = (x - 3)(x + 3)(x - 1)(x + 1)
2. The left behavior is up and the right behavior is up.
  Near x = -3 the graph is positive on the left and negative on the right.
  Near x = -1 the graph is negative on the left and positive on the right
  Near x = 1 the graph is positive on the left and negative on the right.
  Near x = 3 the graph is negative on the left and positive on the right