Polynomial Equations

 

So far we have learned how to find the roots of a polynomial equation.  If we have an equation that involves only polynomials we follow the steps:

Step 1.  Bring all the terms over to the left hand side of the equation so that the right hand side of the equation is a 0.

Step 2.  Get rid of denominators by multiplying by the least common denominator.

Step 3.  If there is a common factor for all the terms, factor immediately.  Otherwise, multiply the terms out.

Step 4.  Use a calculator to locate roots.

Step 5.  Use the Rational Root Theorem and synthetic division to exactly determine the roots.

Example:

Find all the rational solutions of 

        (2x3 - 5)/4 = x - x2

  1. (2x3 - 5)/4 - x + x2 = 0

  2. (2x3 - 5)- 4x + 4x2 = 0

  3. 2x3 + 4x2 - 4x - 5 = 0

  4. From the graph, we see that there is a root between -3 and -2 and a root between 0 and -1 and a root between 1 and 2.  

  5. Since the only possible rational roots are 1, -1, 5, -5, .5, -.5, 2.5, -2.5, the possible rational roots are -5/2 and  -.5.  Neither of these two are roots, hence there are no rational roots.

Example  

Solve  

        x[x2(2x + 3) + 10x + 17] + 5 = 2

  1. x[x2(2x + 3) + 10x + 17] + 3 = 0

  2. 2x4 + 3x3 + 10x2 + 17x + 3 = 0

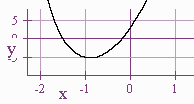
  3. We see that there is a root between -2 and -1 and between -1 and 0.

  4. Our only possible roots are -1/2 and -3/2.

  5. Using synthetic division, we see that -3/2 is a root, and the remainder is

            2x3 + 10x + 2 = 2(x3 + 5x + 1)

which has no rational roots.  Hence the rational root is -3/2 and using the calculator we see that the irrational root is 0.198.

 

Back to Math 103A Home Page

Back to the Math Department Home

e-mail Questions and Suggestions