Lines
-
Lines (definitions)
Everyone knows what a line is, but providing a rigorous definition proves to be a challenge.
Definition
A line with slope m through a point P = (a,b) is the set of all points (x,y) such that
(y - b)/(x - a) = k.
-
The Slope Intercept Form of the equation of a Line
Given a point (x1,y1) and a slope m, the equation of the line is
Slope Intercept Equation of a Line y - y1 = m(x - x1)
-
Piecewise Linear Functions
A function is piecewise linear if it is made up of parts of lines
Example
f (x) = { x + 4 x < -2 2x - 1 -2 < x < 1 -2x 1 < x 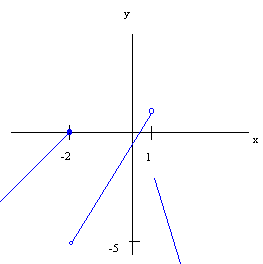
We graph this line by sketching the appropriate parts of each line on the same graph.
Applications
Example
Suppose you own a hotel that has 150 rooms. At $80 per room, you have 140 rooms occupied and for every $5 increase in price you expect to have two additional vacancies. Come up with an equation that gives rooms occupied as a function of price.Solution
Let x be the price of a room and y be the number of rooms occupied. Then we have an equation of a line that passes through the point (80,140) and has slope -1/5. Hence the equation is:
y - 140 = -1/5 (x - 80)
ory = -1/5 x + 16 + 140
or
y = -1/5 x + 156
Exercises
-
What should you do if your two year old daughter has a 40 degree C temperature?
Hint: We have the two points: (0,32) and (100,212)
-
Suppose that your company earned $30,000 five years ago and $35,000 three years ago. Assuming a linear growth model, how much will it earn this year?
-
My rental was bought for $204,000 three years ago. Depreciation is set so that the house depreciates linearly to zero in twenty years from the purchase of the house. If I plan to sell the house in twelve years for $250,000 and capital gains taxes are 28% of the difference between the purchase price and the depreciated value, what will my taxes be?
-
Wasabi restaurant must pay either a flat rate of $400 for rent or 5% of the revenue, whichever is larger. Come up with the equation of the function that relates rent as a function of revenue.
-
Back to the Math Department Home
e-mail Questions and Suggestions