Practice Exam 3
Problem 1 Find the domain of
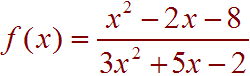
Solution: The domain of a rational function is all the number where the denominator is not equal to 0. We set
3x2 + 5x + 2 = 0
This factors as
(3x + 2)(x + 1) = 0
Solving gives
x = -2/3 or x = -1
Thus the domain is:
Domain = {x|x ≠ -1 and x ≠ -2/3}
Problem 2 The graph is shown below. Find the domain, range, any intercepts, and any asymptotes. Then write down a possible function that has this graph.
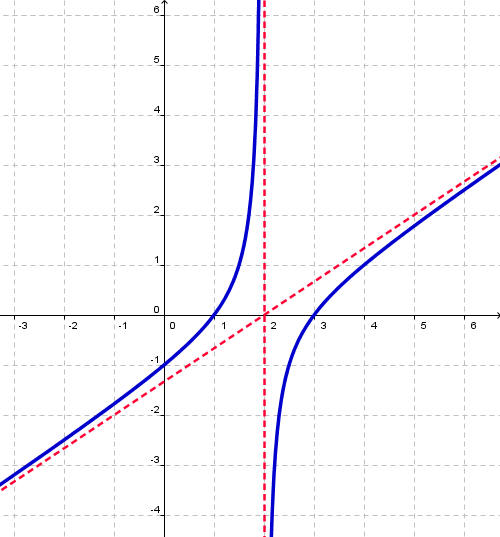
Solution
We can see that there is a vertical asymptote at x = 2. There is an oblique asymptote that passes through the points (2,0) and (5,2). Using the rise over run formula, the slope is
m = 2/3
The equation is
y - 0 = 2/3(x - 2)
or
y = 2/3x - 4/3
The x-intercepts are at the points: (1,0) and (3,0). and the y-intercept is at (0,-1).
Thus the numerator has the factors
(x - 1)(x - 3) = x2 - 4x + 3
The denominator has the factor
(x - 2)
We can set the function to be
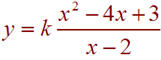
Since the y-intercept is -1, if we plug in 0 for x, we need to get -1 for y. Thus
-1 = k(-3/2)
So that
k = 2/3We leave it up to you that after dividing the polynomials, we get the required oblique asymptote. The answer is
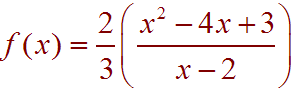
Problem 3 Find all intercepts, holes, and asymptotes of the given rational function then use the information to graph the equation.
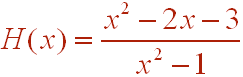
Solution
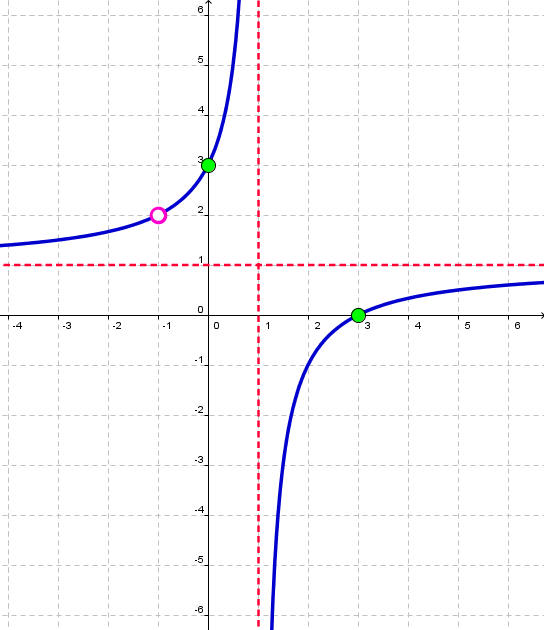
To find the y-intercept, plug in 0 for x. The y-intercept is at (0,3). To find the x-intercept, set the numerator equal to 0 to get
x2 - 2x - 3 = 0
now factor
(x +1)(x - 3) = 0
so that
x = -1 or x = 3
The possible x-intercepts are at the points (-1,0) and (3,0).
To find the vertical asymptotes, set the denominator equal to 0 to get
x2 - 1 = 0
Factoring gives
(x - 1)(x +1) = 0
or
x = -1 or x = 1
Notice that (x +1) is a factor of both the numerator and the denominator. Since the multiplicity of -1 at both the numerator and denominator is 1, we can cancel these factors and conclude that there is a hole at x = -1 and neither an x-intercept nor a vertical asymptote. The function other than the hole is equivalent to
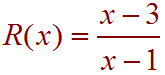
To find the y-coordinate of the hole, just plug in x = -1 into this reduced equation to get y = 2. Thus the hole is at the point (-1,2).
Since the degree of the numerator equals the degree of the denominator, there is a horizontal asymptote. Dividing the highest power terms from the numerator and denominator tells us that the horizontal asymptote has equation y = 1.
We can put all this information together and sketch the graph. It is shown below.
Problem 4 Find all intercepts, holes, and asymptotes of the given rational function then use the information to graph the equation.
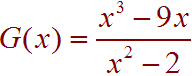
Solution
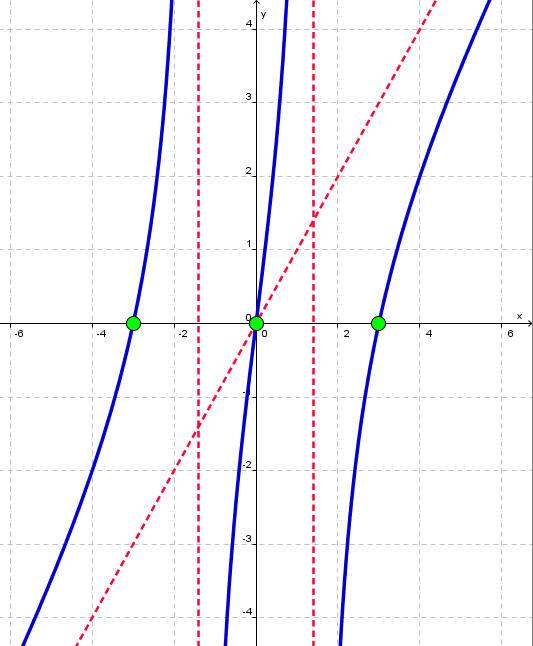
First plug in x = 0 to find the y-intercept. This gives: (0,0). Next factor the numerator to find the x-intercepts. We have
x3 - 9x = x(x2 - 9) = x(x - 3)(x + 3)
So that the x-intercepts are at (-3,0), (0,0), and (3,0). Notice that these do not coincide with zeros of the denominator.
To find the vertical asymptotes, set the denominator equal to 0. This gives the two vertical asymptotes
![]()
Since the degree of the numerator is one more than the degree of the denominator, there is an oblique asymptote. Using polynomial division, we find
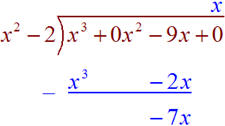
Thus the oblique asymptote is as y = x. We can put this all together to sketch the graph that is shown below.
Problem 5 Use graphical methods to find the solution of
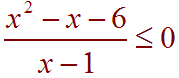
Solution
Find the y-intercept by plugging in 0 for x. We get (0,6). Next factor the numerator as
(x + 2)(x - 3)
to get that the x-intercepts are at (-2,0) and (3,0). This has an oblique asymptote since the degree of the numerator is one greater than the degree of the denominator. Polynomial division yields y = x for this oblique asymptote. There is a vertical asymptote at x = 1. The graph is shown below.
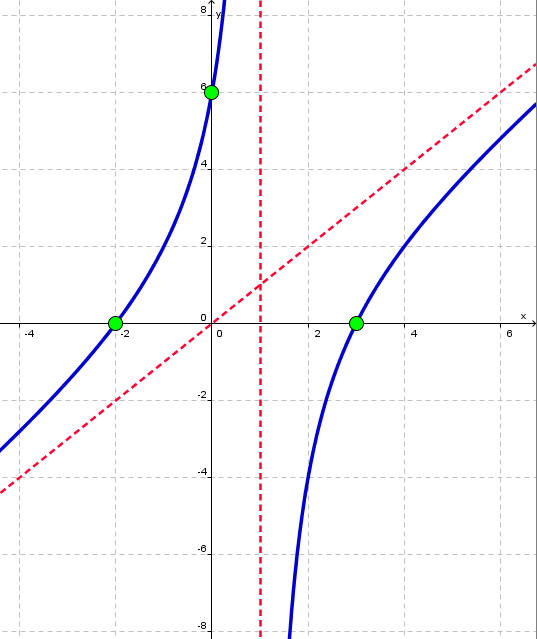
Since the inequality is "<", we want the portions that are on or below the x-axis. The solution is:
![]()
Problem 6 Use Graphical methods to find the solution of
![]()
Solution
We can graph this by looking at the left and right behavior and the roots. This is a degree 9 polynomial with a negative leading coefficient. The roots and their multiplicities are:
x = 0, Multiplicity 2
x = 3, Multiplicity 4
x = -2, Multiplicity 3
Thus the graph touches the x-intercept at 0 and 3 and crosses it at -2. We can put this all together to sketch the graph.
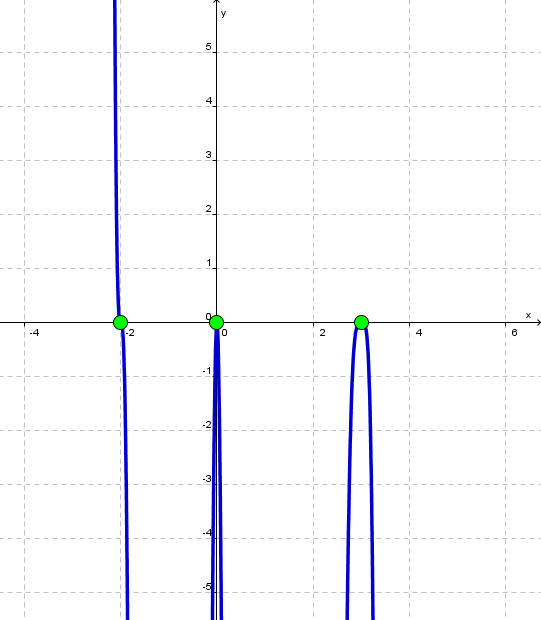
We have the inequality ">". Thus we take the parts that are above the x-axis. The solution is
![]()
Problem 7 Use algebraic methods to find the solution of
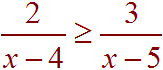
Solution
First set this inequality equal to 0 by subtracting.
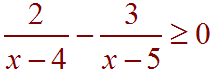
Now put over a common denominator to get
![[2(x-5) - 3(x-4)]/[(x-4)(x-5)] >= 0](img1A.gif)
Simplify the numerator to get
![(-x+2)/[(x-4)(x-5)] >=0](img1F.gif)
The key values are x = 2, x = 4, and x = 5. Next use test points to see if you get a positive or negative value.
| x | -x + 2 | x - 4 | x - 5 | Total |
| 0 | + | - | - | + |
| 3 | - | - | - | - |
| 4.5 | - | + | - | + |
| 6 | - | + | + | - |
Since we have a ">" inequality, we want the positives. The solution is
![]()
Problem 8 Determine the possible number of negative real zeros and the possible number of positive real zeros. Then list the potential rational zeros. Do not attempt to find the zeros.
![]()
Solution
First the degree of f(x) is 8 so there are at most 8 total real roots. To get a bound on the number of positive real roots, we use Descartes Rule of Signs. There are 3 sign changes. Hence there could be 3 or 1 positive real root. To get a bound on the number of negative real roots, change the signs of all of the odd powers:
![]()
Now we count to find 3 sign changes for f(-x). Thus there are 3 or 1 real negative roots also.
Problem 9 Find k such that
![]()
has factor x - 3.
Solution
By the Factor Theorem, if x-3 is a factor, then x = 3 is a root. If we plug in we should get 0.
33 - k(3)2 + k(3) + 2 = 0
Simplifying gives
29 - 6k = 0
Now just solve for k to get
k = 29/6
Problem 10 Factor
![]()
Solution
First factor out an x.
f(x) = x[3x3 - 11x2 + 8x + 4]
By the Rational Root Theorem, any rational roots of the second factor have to be factors of 4 divided by factors of 3. The list is:
1, 2, 4, -1, -2, -4, 1/3, 2/3, 4/3, -1/3, -2/3, -4/3
At this point you can use synthetic division on each of these. The one that works is
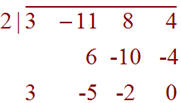
This tells us that
f(x) = x(x-2)(3x2 - 5x - 2)
The last term is just a quadratic and can be factored. The final factored form is
f(x) = x(x-2)(3x + 1)(x - 2)
= x(x - 2)2(3x + 1)
Problem 11 Find a polynomial with a zero at x = 1- i of multiplicity 2 and a zero at x = 4 of multiplicity 3.
Solution
We use the conjugate root theorem that tells us that if 1-i is a root then so is 1+i. Thus f can be factored as
f(x) = (x - (1+i))2 (x - (1-i))2 (x-2)3
= [((x - 1) + i)((x - 1) - i)]2(x - 2)3
= [(x - 1)2 + 1]2(x - 2)3
= [x2 - 2x + 2]2(x - 2)3
Problem 12 One of the roots of the polynomial below is 3-i. Find the rest of the roots.
![]()
The Conjugate root theorem tells us that a second root is 3 + i. Thus two factors are
(x - (3 + i))(x - (3 - i)) = ((x - 3) - i)((x -3) + i)
= (x - 3)2 + 1
= x2 - 6x + 10
Now divide the polynomials to get the other factor
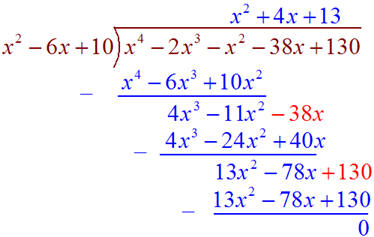
Thus the function can be factored as
f(x) = (x2 - 6x + 10)(x2 + 4x + 13)
We can use the quadratic formula on the second factor to find that the other two roots are -2 + 3i and -2 - 3i. In summary, the four roots are
3 - i, 3 + i, -2-3i, and -2 + 3i
Problem 13 Find the zeros (real and complex) of the function. Then write the function in factored form.
![]()
Solution
First notice that by Descartes Rule of Signs, there are no positive real roots (no sign changes). The only possible rational roots (by the Rational Root Theorem) are
-1, -5, -13, -65
You can plug in -1 and quickly see that -1 is not a root. Using synthetic division with the root -5 gives

This tells us that that the polynomial factors as
f(x) = (x - 5)(x2 + 6x + 13)
Now we can use the quadratic formula to find that the other two roots are -3 + 2i and -3 - 2i. In conclusion, the three roots are
-5, -3 + 2i, and -3 - 2i