MAT 103B Practice Final Key

No Calculators Portion

Problem 1.  Use transformations to sketch the graph.  Then state the domain and range.

A.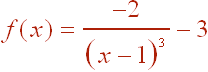 

Solution

We see that the graph looks like the y = 1/x³ curve, but is shifted 1 to the right and 3 downward.  The effect of the -2 is to reflect the graph across the y-axis and stretch by a factor of 2.  The key point (1,1) becomes (2,-5).  The vertical asymptote x = 0 also shifts 1 to the right and becomes x = 1.  The horizontal asymptote y = 0 also shifts downward to y = -3.  The graph is shown below.

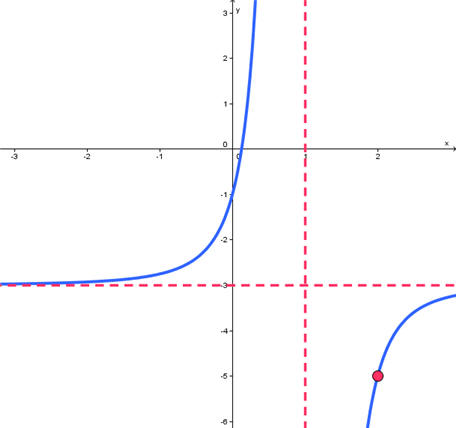
The domain is the set of all values of x that are included on the graph.  Notice that the graph comes from the far left and goes to the far right.  The only issue is the vertical asymptote at x = 1.  Thus the domain is

Domain = {x|x ≠ 1}

The range is the set of all values of y  that are included in the graph.  Notice that the graph comes from way below and goes way above.  The graph does not cross the horizontal asymptote, thus the range does not include y = -3.  Thus the range is

Range = {y| y ≠ -3}

B. 

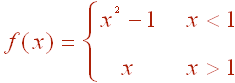
This is a piecewise function that is parabolic to the left of x = 1 and linear to the right of x = 1.  Since neither pieces have "equal" as part of the inequality, there is a hole at the right end of the parabolic piece at (1,0) and a hole at the beginning of the linear piece at (1,1).  The graph is shown below.

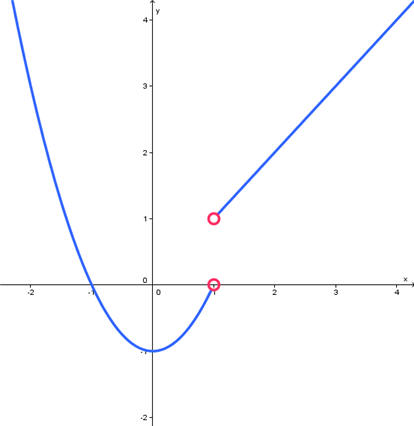
The domain is the set of all values of x that are included on the graph.  Notice that the graph comes from the far left and goes to the far right.  The only issue is that x is undefined at 1.  Thus the domain is

Domain = {x|x ≠ 1}

The range is the set of all values of y  that are included in the graph.  Notice that the graph comes from way below and goes way above.  The graph does not cross the horizontal asymptote, thus the range does not include y = -3.  Thus the range is

Range = {y| y > -1}

Problem 2.  Find the domain of the function

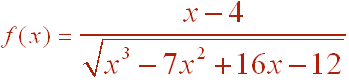
Solution

The issue is that the denominator cannot be 0 and the expression under the square root must not be negative.  This gives

x³ -7x² + 16x - 12  > 0

We need to factor this polynomial.  Be Descartes rule of signs, there are no negative roots.  By the rational root theorem the only possible roots (which must be positive) are

1, 2, 3, 4, 6, 12

By plugging in 1, we see that 1 is not a root.  Let's try 2:

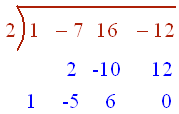
Thus 2 is a root and the factored form so far is

(x - 2)(x² - 5x + 6)

Now factor the last factor to get

(x - 2)(x - 2)(x - 3)

or

(x - 2)²(x-3) > 0

We can use the test points:

x  =  0:  (+)(-)  =  -

x  =  2.5:  (+)(-)  =  -

x  =  4:  (+)(+)  =  +

Since the inequality is ">", we want the "+" regions.  Thus the solution is

{x | x > 3}

Problem 3.  List the intercepts and test for symmetry

Solution

To find the x intercept, set y = 0 and solve

-4x² = 36

has not solution, so this has no x intercepts.  To to find the y intercepts, set x = 0 and solve

9y² = 36

Divide by 9 and take a square root to get y = -2 or y = 2.  We get the point (0,-2) and (0,2) for the y intercepts.

Now test for symmetry.  To test for y-axis symmetry, replace x with -x and see if the equation stays the same.  We have

9y² - 4(-x)²  =  36

Since the square kills the "-" sign this is equivalent to

9y² - 4x²  =  36

Thus the graph is symmetric about the y-axis.

Now test for x-axis symmetry.  Replace y with -y and see if the equation stays the same.  We have

9(-y)² - 4x²  =  36

Again the square kills the "-" sign and the equation is equivalent to

9y² - 4x²  =  36

Thus the graph is symmetric to the x-axis.  A graph that is symmetric to both the x-axis and the y-axis is also symmetric to the origin.

Problem 4.  Determine if the graph of the quadratic function is concave up or down, find the vertex, intercepts and axis of symmetry, and where the function is increasing and where it is decreasing.  Then use this information to sketch a graph of the function.

Solution

Since the leading coefficient (-3) is negative the graph is concave down.  Plug in x = 0 to find the y-intercept of (0,24).  Next set this equation equal to 0 and solve

-3x² + 6x + 24  =  0

Divide by -3 to get

x² - 2x - 8  =  0

Factoring gives

(x + 2)(x - 4)  =  0

So that the x intercepts are at (-2,0) and (4,0).

To find the vertex use the formula

v_x = (b/2a)²  =  (6/-6)²  =  1

To find the y coordinate of the vertex, plug x = 1 into the original equation to get

y  =  -3(1)² + 6(1) + 24

   =  27

Thus the vertex is at the point (1,27).

The axis of symmetry is the x coordinate of the vertex or x = 1.  Since the graph is concave down, the function is increasing from negative infinity to the x coordinate of the vertex and it is decreasing from the x coordinate of the vertex to infinity.  The graph is shown below.

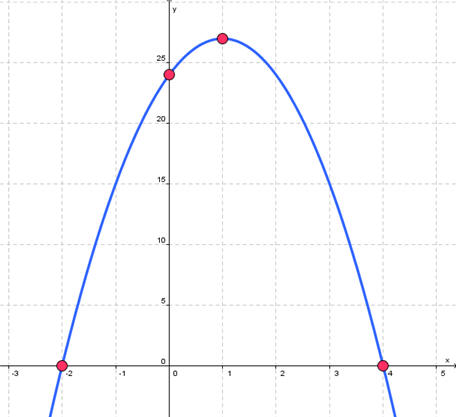
Problem 5.  List the real zeros, determine whether the function crosses or touches the x-axis at each intercept, determine the maximum number of turning points on the graph, determine the left and right behavior, then use the information to sketch a possible graph.

Solution

The zeros are at x = 0, x = 2, and x = 1.  Recall the if the multiplicity (power) of the root is odd then the graph crosses the x-axis there and if it is even then the graph touches the x-axis there.  Thus the graph crosses the x-axis at x = -1 and at x = 2.  It touches the x-axis at x = 0.  The degree of the polynomial is the sum of the powers or

Degree  =  2 + 3 + 1  =  6

The number of turning points is always less than the degree, hence the maximum number of turning points for this graph is 5.  Since the degree is even (6) and the leading coefficient is negative, the left and right behavior is the same as the left and right behavior of y = -x².  That is it goes steeply downward towards negative infinity on both the left and right hand side of the graph.  The graph is shown below.

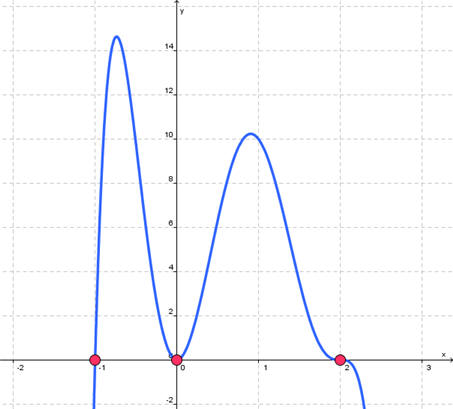
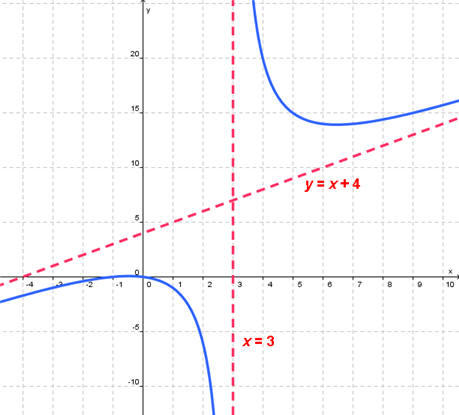
Problem 6.  Sketch the graph of the rational function.

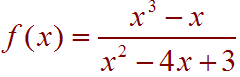
Solution

This is a rational equation.  First find the y-intercept by plugging in 0 for x to get the point (0,0).  Next factor the numerator and the denominator as

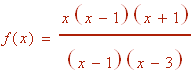
Notice that both numerator and denominator have the same factor.  Thus there is a hole at x = 1.  Other than the hole, the graph will be the same as the graph of

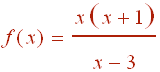
The x-intercepts of the graph are at (0,0) and (-1,0).  The vertical asymptote is at x = 3.  Plugging in x = 1 into the reduced equation gives y = -1.  Thus the hole is at the point (1,-1).  Since the degree of the numerator is one greater than the degree of the denominator, there will be an oblique asymptote.  Multiply the numerator through and use synthetic division to get

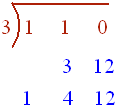
Thus the oblique asymptote is at

y  =  x + 4

The remainder is the constant 12 which is never 0, thus the graph does not cross the oblique asymptote.  Now we just sketch

Problem 7.  Use algebraic methods to find the roots of

Solution

By Descartes rule of signs, there are no positive real roots.  By the rational root theorem the possible rational roots are

-1, -2, -3, -4, -6, -12, -1/2, -3/2

After trying x = -1 and finding out that it is not a root, we try x = -2:

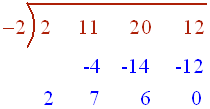
We see that -2 is a root since the remainder is 0.  We get

f(x)  =  (x - 2)(2x² + 7x + 6)

This factors as

f(x)  =  (x + 2)(x + 2)(2x + 3)

Thus there is a root at x = -2 of multiplicity 2 and a root at x = -3/2 of multiplicity 1.

Problem 8.  Form a polynomial with real coefficients having the given degree and zeros. 

Degree 7:  The only real zero is -3.  Complex zeros include 3i and 1+2i.

We use the conjugate root theorem to conclude that there are also roots at -3i and 1 - 2i.  Since the degree is 7 and we have found 5 roots, we can make the root of -3 have multiplicity 3 to get 7 roots including multiplicity.  Thus the polynomial has factored form

(x + 3)³ (x - 3i)(x + 3i)(x - (1 + 2i))(x - (1 - 2i))

Now multiply the second two factors and rearrange the parentheses to get

=  (x + 3)³ (x² + 9)((x - 1) - 2i)((x - 1) + 2i))

The last two factors are comprise a difference of squares to give

=  (x + 3)³ (x² + 9)((x - 1)²  + 4)

=  (x + 3)³ (x² + 9)(x² - 2x + 5)

With Calculators Portion

Problem 9.  Find the distance between the point (5,1) and the maximum point on the graph of

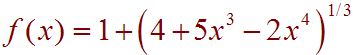
First use a calculator to find the maximum point on the graph.  The calculator obtained:

(1.875, 3.30457)

Now use the distance formula

Problem 10.  The data describes the amount spent x (in thousands of dollars) on advertising vs. revenue y  (in thousands of dollars)  for a business.  Determine whether a linear model or a quadratic model should be used.  Then find the equation for this model.  Use your equation to predict the revenue if a business spends $3000 on advertising.  If the model is linear, interpret the slope and y-intercept.

Solution

We can use a calculator to plot the scatter diagram.  The diagram is shown below

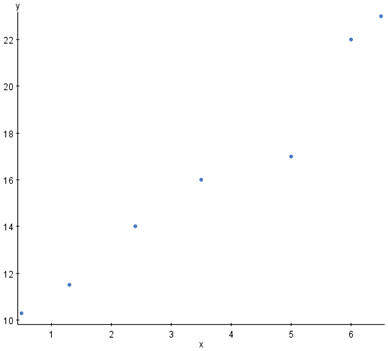
Since this scatter diagram look closer to being linear than parabolic, we use the linear regression equation.  The calculator gives

y  =  8.88 + 2.05x

If we plug in 3 for x, we get

y  =  8.88 + 2.05(3) 

   =  15.03

or we can predict that the revenue for the company is predicted to be around $15,000 when $3,000 is spent on advertising.

The slope is about 2, which means that if the advertising money is increased by $1,000, then the revenue is predicted to increase by $2,000.

The y-intercept is 8.88 which means that the predicted revenue if there is no money spent on advertising, then the expected revenue is $8,880.

Problem 11.  A track and field playing area is in the shape of a rectangle with semicircles at each end.  The perimeter of the track is to be 1200 meters.  What should the dimensions of the rectangle be so that the area of the rectangle is a maximum?

Solution

The perimeter consists of two semi-circles (that make up a complete circle and two sides.  If we let the radius of the semi-circles be r and x be the straight path on the bottom of the track, then the perimeter will be

Perimeter  =  2x + 2pr  =  1200

The area of the rectangle is

Area  =  (x)(2r)

Solve the perimeter equation for x to get

x  =  600 - pr

Substitute this into the area equation to get

Area  =  (600 - pr)(2r)

Putting this into a calculator (this can also be done by hand using the vertex of a parabola formula) to find the maximum gives

r = 95.493  and   Area = 57,295.8

We want the dimensions of the rectangle, so we need the base and the height.  The height is twice the radius or 190.986.  To find the base, x, we can use the equation

x  =  600 - p(95.493)

   =  300 

Thus the dimensions of the rectangle are 300 by 190.986.

Problem 12.  One of the vertices of a rectangle is at the origin.  Another is on the curve y = 4 - x² in the first quadrant.  Find the dimensions of the largest rectangle that can be constructed in this way.

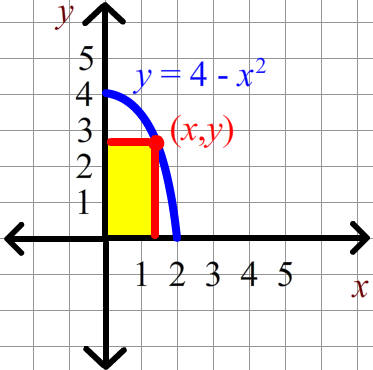
Solution

We find the area of the rectangle which is the base times the height.  The base is x and the height is y.  We can substitute in the equation of the curve to get

Area  =  xy  =  x(4 - x²)

We can put this into the calculator and find the maximum at x = 1.1547.  We can put this into the equation for y to get

y  =  4 - (1.1547)²

   =  2.6667 

Thus the dimensions of the rectangle are 1.1547 by 2.6667.